【题目】已知矩形ABCD,AB=10,BC=13,点P为边AD上一动点,点A’与点A关于BP对称,连结A’C,当△A’BC为等腰三角形时,AP的长度为()

A.2B.![]() C.2或
C.2或![]() D.2或
D.2或![]()
参考答案:
【答案】C
【解析】
①如图1,当A′B=A′C时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,得到MN垂直平分BC和AD,根据轴对称的性质得到AB=A′B=10,∠PA′B=∠A=90°,根据勾股定理得到A′M=![]() ,根据相似三角形的性质即可得到结论;②当A′B=BC时,这种情况不存在;③如图2,当A′C=BC=13时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,由勾股定理得到CH=
,根据相似三角形的性质即可得到结论;②当A′B=BC时,这种情况不存在;③如图2,当A′C=BC=13时,过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,由勾股定理得到CH=![]() ,根据三角形的面积公式得到A′M=
,根据三角形的面积公式得到A′M=![]() ,根据相似三角形的性质即可得到结论.
,根据相似三角形的性质即可得到结论.
解:∵△A′BC为等腰三角形,
∴①如图1,当A′B=A′C时,过A′作A′M⊥BC于M反向延长A′M交AD于N,
则MN⊥AD,
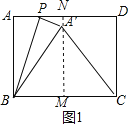
∴MN垂直平分BC和AD,
∵BC=13,
∴BM=AN=![]() ,
,
∵点A′与点A关于BP对称,
∴△ABP≌△A′BP,
∴AB=A′B=10,∠PA′B=∠A=90°,
∴A′M=![]() ,
,
∴A′N=MN-A′M=![]() ,
,
∵∠PA′N+∠A′PN=∠PA′N+∠BA′M=90°,
∴∠A′PN=∠BA′M,
∵∠PNA′=∠A′MB=90°,
∴△A′PN∽△BA′M,
∴![]() ,
,
∴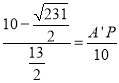 ,
,
∴A′P=![]() ,
,
∴AP=A′P=![]() ,
,
②当A′B=BC时,
∵A′B=AB=10,
∴这种情况不存在;
③如图2,当A′C=BC=13时,
过A′作A′M⊥BC于M反向延长A′M交AD于N,则MN⊥AD,过C作CH⊥A′B于H,
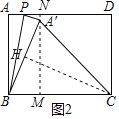
∴BH=![]() ×10=5,
×10=5,
∴CH=![]() ,
,
∴A′M=![]() ,
,
∴A′N=![]() ,BM=
,BM=![]() ,
,
由①知,![]() ,
,
∴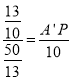 ,
,
∴A′P=AP=2,
综上所述,AP的长度为2或![]() ;
;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(1,a)是直线y1=2x与双曲线y2=
 在第一象限的交点.
在第一象限的交点.(1)求双曲线的解析式;
(2)直接写出当y1>y2时,自变量的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列给出的条件中,能判定四边形ABCD为平行四边形的是()
A.AB=BC,CD=DAB.AB//CD,AD=BC
C.AB//CD,∠A=∠CD.∠A=∠B,∠C=∠D
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD,∠A=60°,AB=6,点M从点D向点A以1个单位∕秒的速度运动,同时点N从点D向点C以2个单位∕秒的速度运动,连结BM、BN,当△BMN为等边三角形时,
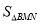 =_____.
=_____.
-
科目: 来源: 题型:
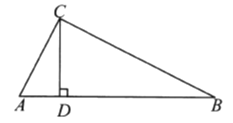
查看答案和解析>>【题目】如图,在
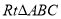 中,
中, 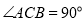 ,CD是斜边AB上的高.
,CD是斜边AB上的高.(1)证明:
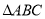 ∽
∽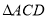
(2)写出除(1)外的另两对相似三角形.
(3)AC是哪两条线段的比例中项?请简要证明(说明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车站在春运期间为改进服务,抽查了100名旅客从开始在窗口排队到购到车票所用时间t(以下简称购票用时,单位:分),得到如下表所示的频数分布表.
分组
频数
一组
0≤t<5
0
二组
5≤t<10
10
三组
10≤t<15
10
四组
15≤t<20
五组
20≤t<25
30
合计
100
(1)在表中填写缺失的数据;
(2)画出频数分布直方图;
(3)旅客购票用时的平均数可能落在哪一小组内?
(4)若每增加一个购票窗口可以使平均购票用时降低5分,要使平均购票用时不超过10分,那么请你决策一下至少要增加几个窗口?
相关试题

