【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)利用直角三角形斜边中线是斜边一半,求得DE=AE=AF=DF,
所以AEDF是菱形.
(2)由(1)得,AEDF是菱形,求得菱形对角线乘积的一半,求面积 .
试题解析:
(1)∵AD⊥BC,点E、F分别是AB、AC的中点,
∴Rt△ABD中,DE=![]() AB=AE,
AB=AE,
Rt△ACD中,DF=![]() AC=AF,
AC=AF,
又∵AB=AC,点E、F分别是AB、AC的中点,
∴AE=AF,
∴AE=AF=DE=DF,
∴四边形AEDF是菱形.
(2)如图,∵菱形AEDF的周长为12,
∴AE=3,
设EF=x,AD=y,则x+y=7,
∴x2+2xy+y2=49,①
∵AD⊥EF于O,
∴Rt△AOE中,AO2+EO2=AE2,
∴(![]() y)2+(
y)2+(![]() x)2=32,
x)2=32,
即x2+y2=36,②
把②代入①,可得2xy=13,
∴xy=![]() ,
,
∴菱形AEDF的面积S=![]() xy=
xy=![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣3x2xy= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.
图象的顶点坐标为(3,8),该二次函数图象的对称轴与x轴的交点为A,M是这个二次函数图象上的点,O是原点.(1)不等式b+2c+8≥0是否成立?请说明理由;
(2)设S是△AMO的面积,求满足S=9的所有点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题“如果两个角是直角,那么它们相等”的逆命题是 ;逆命题是 命题(填“真”或“假”).
-
科目: 来源: 题型:
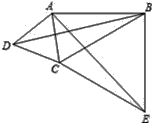
查看答案和解析>>【题目】如图,在四边形ABCD中,∠ABC=30°,∠ADC=60°,AD=DC,连结AC、BD.在四边形ABCD的外部以BC为一边作等边△BCE,连结AE.
(1)求证:BD=AE;
(2)若AB=3,BC=4,求BD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、D、C三点在一条直线上,∠ADB=∠ADC=90°,BD=DE,∠DAC=45°;
(1)线段AB、CE的关系为 ;
(2)若BD=a,AD=b,AB=c,请利用此图的面积式证明勾股定理.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+y2=10,xy=2,则(x+y)2= .
相关试题

