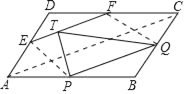
【题目】如图,在ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与ABCD的面积之比是______.

参考答案:
【答案】1:4
【解析】
如图,连接AC、PE、QF.设平行四边形ABCD的面积为8S,证明四边形EFQP是平行四边形,求出S平行四边形EFQP=4S和S△TPQ=2S即可解决问题.
解:如图,连接AC、PE、QF.设平行四边形ABCD的面积为8S.
∵DE=AE,DF=FC,
∴EF∥AC,EF:AC=1:2,
∴S△DEF=![]() S△DAC=
S△DAC=![]() ×4S=S,
×4S=S,
同理可证PQ∥AC,PQ:AC=1:2,S△CFQ=S△PQB=S△APE=S,
∴四边形EFQP是平行四边形,
∴S平行四边形EFQP=4S,
∴S△TPQ=![]() S平行四边形EFQP=2S,
S平行四边形EFQP=2S,
∴S△TPQ:S平行四边形ABCD=2S:8S=1:4,
故答案为1:4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2013年安庆市体育考试跳绳项目为学生选考项目,下表是某班模拟考试时10名同学的测试成绩(单位:个/分钟),则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
A. 众数是177 B. 平均数是170 C. 中位数是173.5 D. 方差是135
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(如图1所示)在△ABC中,∠ACB=90°,∠A=30°,BC=4,沿斜边AB的中线CD把这个三角形剪成△AC1D1和△BC2D2两个三角形(如图2所示).将△AC1D1沿直线D2B方向平移(点A,D1,D2,B始终在同一直线上),当点D1于点B重合时,平移停止.设平移距离D1D2为x,△AC1D1和△BC2D2的重叠部分面积为y,在y与x的函数图象大致是( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,DE垂直平分BC,垂足为点D,交AB于点E,且AD=AC,EC交AD于点F,下列说法:
①△ABC∽△FDC;②点F是线段AD的中点;③S△AEF:S△AFC=1:4;④若CE平分∠ACD,则∠B=30°,其中正确的结论有_____(填写所有正确结论的序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四点A、B、C、D;
(1)画射线AD;(不需写作图过程)
(2)求作点P,使PA+PB+PC+PD的值最小;(不需写作图过程)
(3)在(2)的条件下,若S△ABP=2,S△ADP=6,S△BCP=1.5,则S△DCP= .
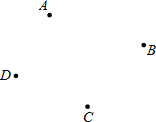
-
科目: 来源: 题型:
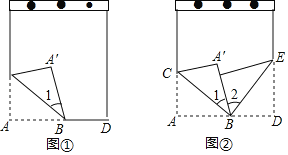
查看答案和解析>>【题目】如图①,将笔记本活页一角折过去,使角的顶点A落在A′处,BC为折痕;
(1)图①中,若∠1=30°,则∠A′BD=_____;
(2)如果在图②中改变∠1的大小,则BA的位置也随之改变,又将活页的另一角斜折过去,使BD边与BA′重合,折痕为BE.那么∠CBE的度数是否会发生变化呢?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的顶点坐标分别为A(1,3),B(4,2),C(2,1).
(1)作出与△ABC关于x轴对称的△A1B1C1.
(2)以原点O为位似中心,在原点的另一个侧画出△A2B2C2.使
 =
= ,并写出A2、B2、C2的坐标.
,并写出A2、B2、C2的坐标.
相关试题

