[题目]2013年安庆市体育考试跳绳项目为学生选考项目.下表是某班模拟考试时10名同学的测试成绩(单位:个/分钟).则关于这10名同学每分钟跳绳的测试成绩.下列说法错误的是( ) 成绩(个/分钟)140160169170177180人数111232A. 众数是177 B. 平均数是170 C. 中位数是173.5 D. 方差是135 题目和参考答案 ——青夏教育精英家教网—

【题目】2013年安庆市体育考试跳绳项目为学生选考项目，下表是某班模拟考试时10名同学的测试成绩（单位：个/分钟），则关于这10名同学每分钟跳绳的测试成绩，下列说法错误的是（　　）

成绩（个/分钟）	140	160	169	170	177	180
人数	1	1	1	2	3	2

A. 众数是177 B. 平均数是170 C. 中位数是173.5 D. 方差是135

参考答案：

【答案】D

【解析】A、这组数据中177出现次数最多，即众数为177，此选项正确；

B、这组数据的平均数是：（140+160+169+170×2+177×3+180×2）÷10=170，此选项正确；

C、∵共有10个数，

∴中位数是第5个和6个数的平均数，

∴中位数是（170+177）÷2=173.5；此选项正确；

D、方差= [（140﹣170）2+（160﹣170）2+（169﹣170）2+2×（170﹣170）2+3×（177﹣170）2+2×（180﹣170）2]=134.8；此选项错误；

故选：D．

相关试题

科目： 来源： 题型：

【题目】课本中有一探究活动：如图1，有甲、乙两个三角形，甲三角形内角分别为10°，20°，150°；乙三角形内角分别为80°，25°，75°．你能把每一个三角形分成两个等腰三角形吗？画一画，并标出每个等腰三角形顶角的度数．
（1）小明按要求画出了图1中甲图的分割线，请你帮他作出图1中乙图的分割线；
（2）小明进一步探究发现：能将一个顶角为108°的等腰三角形分成三个等腰三角形；请在图2中用两种不同的方法画出分割线，并标注每个等腰三角形顶角的度数；（若两种方法分得的三角形成3对全等三角形，则视为同一种方法）
查看答案和解析>>
科目： 来源： 题型：

【题目】已知：如图，在梯形ABCD中，AB∥CD，∠D=90°，AD=CD=2，点E在边AD上（不与点A、D重合），∠CEB=45°，EB与对角线AC相交于点F，设DE=x．
（1）用含x的代数式表示线段CF的长；
（2）如果把△CAE的周长记作C△CAE，△BAF的周长记作C△BAF，设=y，求y关于x的函数关系式，并写出它的定义域；
（3）当∠ABE的正切值是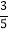时，求AB的长．
查看答案和解析>>
科目： 来源： 题型：

【题目】将一副三角板中的两块直角三角板的直角顶点C按如图方式叠放在一起，友情提示：∠A＝60°，∠D＝30°，∠E＝∠B＝45°．
(1)①若∠DCB＝45°，则∠ACB的度数为　　．
②若∠ACB＝140°，则∠DCE的度数为　　．
(2)由(1)猜想∠ACB与∠DCE的数量关系，并说明理由．
(3)当∠ACE＜90°且点E在直线AC的上方时，当这两块三角尺有一组边互相平行时，请直接写出∠ACE角度所有可能的值(不必说明理由)．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图（如图1所示）在△ABC中，∠ACB=90°，∠A=30°，BC=4，沿斜边AB的中线CD把这个三角形剪成△AC1D1和△BC2D2两个三角形（如图2所示）．将△AC1D1沿直线D2B方向平移（点A，D1，D2，B始终在同一直线上），当点D1于点B重合时，平移停止．设平移距离D1D2为x，△AC1D1和△BC2D2的重叠部分面积为y，在y与x的函数图象大致是（　　）
A. B. C. D.
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在△ABC中，DE垂直平分BC，垂足为点D，交AB于点E，且AD=AC，EC交AD于点F，下列说法：
①△ABC∽△FDC；②点F是线段AD的中点；③S△AEF：S△AFC=1：4；④若CE平分∠ACD，则∠B=30°，其中正确的结论有_____（填写所有正确结论的序号）．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在ABCD中，分别设P，Q，E，F为边AB，BC，AD，CD的中点，设T为线段EF的三等分点，则△PQT与ABCD的面积之比是______．
查看答案和解析>>