【题目】平面直角坐标系中,有A、B、C三点,其中A为原点,点B和点C的坐标分别为(5,0)和(1,2).
(1)证明:△ABC为RT△;
(2)请你在直角坐标系中找一点D,使得△ABC与△ABD相似,写出所有满足条件的点D的坐标,并在同一坐标系中画出所有符合要求的三角形;
(3)在第(2)题所作的图中,连接任意两个直角三角形(包括△ABC)的直角顶点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,求取到长度为无理数的线段的概率.
参考答案:
【答案】(1)证明见解析;(2)D1(1,-2);D2(4,-1),D3(4,1);D4(5,-10),D5(5,10);D6(5,-2.5),D7(5,2.5);D8(0,-10),D9(0,10);D10(0,-2.5),D11(0,2.5);作图见解析;(3)p=![]() .
.
【解析】
试题分析:本题主要考查了勾股定理及其逆定理、相似三角形的性质、概率公式等知识,运用分类讨论的思想是解决第(2)小题的关键.
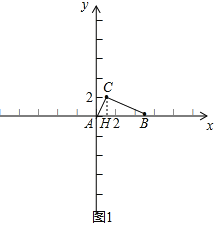
(1)过点C作CH⊥x轴于H,如图1,只需运用勾股定理求出AB2、AC2、BC2,然后运用勾股定理的逆定理就可解决问题;
(2)△ABC与△ABD相似,对应关系不确定,故需分六种情况(①若△ABC∽△ABD,②若△ABC∽△BAD,③若△ABC∽△ADB,④若△ABC∽△DAB,⑤若△ABC∽△BDA,⑥若△ABC∽△DBA)讨论,然后运用相似三角形的性质就可解决问题;
(3)图中的直角三角形的直角顶点有A、B、C、D1、D2、D3,只需求出任意两直角顶点的连线段的条数和长度为无理数的线段的条数,就可解决问题.
试题解析:(1)过点C作CH⊥x轴于H,如图1,
∵A(0,0),B(5,0),C(1,2),
∴AC=![]() ,BC=2
,BC=2![]() ,AB=5,
,AB=5,
∴AB2=AC2+BC2,
∴△ABC为RT△;
 ;
;
(2)①若△ABC∽△ABD,则有D1(1,-2);
②若△ABC∽△BAD,则有D2(4,-1),D3(4,1);
③若△ABC∽△ADB,则有D4(5,-10),D5(5,10);
④若△ABC∽△DAB,则有D6(5,-2.5),D7(5,2.5);
⑤若△ABC∽△BDA,则有D8(0,-10),D9(0,10);
⑥若△ABC∽△DBA,则有D10(0,-2.5),D11(0,2.5);
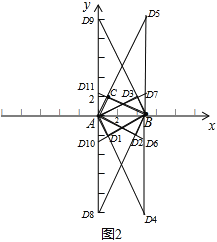
所有符合要求的三角形如图2所示:
 ;
;
(3)图中的直角三角形的直角顶点有A、B、C、D1、D2、D3.
任意两直角顶点的连线段共有6×52=15条,
其中AB=5,CD1=D2D3=4,CD2=D1D3=5,CD3=D1D2=3,
故长度为有理数的线段共7条,长度为无理数的线段共8条,
则取到长度为无理数的线段的概率为p=![]() .
.
-
科目: 来源: 题型:
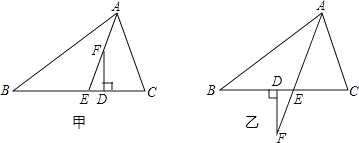
查看答案和解析>>【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=
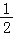 (∠C﹣∠B);
(∠C﹣∠B);(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1过点A(8,0)、B(0,﹣5),直线l2过点C(0,﹣1),l1、l2相交于点D,且△DCB的面积等于8.
(1)求点D的坐标;
(2)点D的坐标是哪个二元一次方程组的解.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G.图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
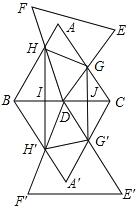
(1)求证:△DHB∽△GDC;
(2)设CG=x,四边形HH′G′G的面积为y,
①求y关于x的函数解析式和自变量x的取值范围;
②求当x为何值时,y的值最大,最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 绝对值等于本身的数是1、-1、0
B. 一个负数的绝对值是它的相反数
C. 如果两个数的绝对值相等,那么这两个数相等
D. 平方等于9的数是3
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:71=7,72=49,73=343,74=2401,75=16807,…那么72007+1的个位数字是( )
A. 8 B. 4 C. 2 D. 0
-
科目: 来源: 题型:
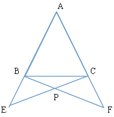
查看答案和解析>>【题目】在△ABC中,AB=AC,点E,F分别在AB,AC的延长线上,AE=AF,BF与CE相交于点P,求证:PB=PC,并请直接写出图中其他相等的线段.
相关试题

