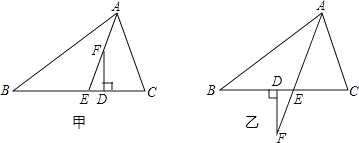
【题目】已知,如图甲,在△ABC中,AE平分∠BAC(∠C>∠B),F为AE上一点,且FD⊥BC于D.
(1)试说明:∠EFD=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)当F在AE的延长线上时,如图乙,其余条件不变,(1)中的结论还成立吗?请说明理由.
参考答案:
【答案】(1) 见解析;(2) 成立,理由见解析.
【解析】试题分析:(1) 根据三角形内角和定理以及角平分线的定义得到∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)=90°﹣
(180°﹣∠B﹣∠C)=90°﹣![]() (∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;(2)根据(1)可以得到∠AEC=90°+
(∠B+∠C),然后根据三角形的外角的性质可以得到∠FEC=∠B+∠BAE,求得∠FEC,再根据直角三角形的两个锐角互余即可求得结论;(2)根据(1)可以得到∠AEC=90°+![]() (∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
(∠B﹣∠C),根据对顶角相等即可求得∠DEF,然后利用直角三角形的两个锐角互余即可求解.
试题解析:
解:(1)∵AE平分∠BAC,
∴∠BAE=![]() ∠BAC=
∠BAC=![]() (180°﹣∠B﹣∠C)
(180°﹣∠B﹣∠C)
=90°﹣![]() (∠B+∠C),
(∠B+∠C),
∵∠FEC=∠B+∠BAE,
则∠FEC=∠B+90°﹣![]() (∠B+∠C)
(∠B+∠C)
=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∵FD⊥EC,
∴∠EFD=90°﹣∠FEC,
则∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B);
(∠C﹣∠B);
(2)成立.
证明:同(1)可证:∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠DEF=∠AEC=90°+![]() (∠B﹣∠C),
(∠B﹣∠C),
∴∠EFD=90°﹣[90°+![]() (∠B﹣∠C)]
(∠B﹣∠C)]
=![]() (∠C﹣∠B).
(∠C﹣∠B).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果数轴上的点A对应的数为3,那么与A点相距200个单位长度的点所对应的有理数为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直角三角形的两条直角边长分别为6和8,则它的外接圆的半径为___
-
科目: 来源: 题型:
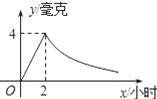
查看答案和解析>>【题目】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题.
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1过点A(8,0)、B(0,﹣5),直线l2过点C(0,﹣1),l1、l2相交于点D,且△DCB的面积等于8.
(1)求点D的坐标;
(2)点D的坐标是哪个二元一次方程组的解.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G.图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
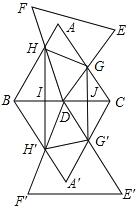
(1)求证:△DHB∽△GDC;
(2)设CG=x,四边形HH′G′G的面积为y,
①求y关于x的函数解析式和自变量x的取值范围;
②求当x为何值时,y的值最大,最大值为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,有A、B、C三点,其中A为原点,点B和点C的坐标分别为(5,0)和(1,2).
(1)证明:△ABC为RT△;
(2)请你在直角坐标系中找一点D,使得△ABC与△ABD相似,写出所有满足条件的点D的坐标,并在同一坐标系中画出所有符合要求的三角形;
(3)在第(2)题所作的图中,连接任意两个直角三角形(包括△ABC)的直角顶点均可得到一条线段,在连接两点所得的所有线段中任取一条线段,求取到长度为无理数的线段的概率.
相关试题

