搜索
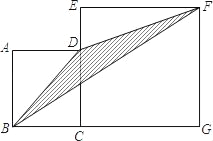
【题目】如图，四边形ABCD和四边形EFBC均为正方形，点D在EC上．如果线段AB的长为5，则△BDF的面积为_____．
参考答案：
【答案】12.5
【解析】
设出正方形EFCG的边长为a，表示出ED与BG，求出三角形EFD的面积，由正方形EFCG的面积-三角形EFD的面积得到四边形DCGF的面积，求出三角形BCD的面积，三角形BDF面积=三角形BCD面积+四边形DCGF的面积-三角形BGF的面积，求出即可．
设正方形EFGC的边长为a，即EC=EF=CG=FG=a，
∴ED=ECDC=a5，BG=BC+CG=a+5，
∴S△EFD=12a(a5)，
∴S四边形DCGF=a212a(a5)，
∵S△BCD=12×52=12.5,S△BCF=12a(a+5)，
∴S△BDF=S△BCD+S四边形DCGFS△BCF=12.5+a212a(a5)12a(a+5)=12.5，
故答案为：12.5.
-
科目： 来源： 题型：
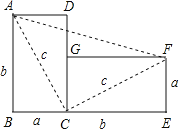
查看答案和解析>>【题目】如图，将边长为a与b、对角线长为c的长方形纸片ABCD，绕点C顺时针旋转90°得到长方形FGCE，连接AF．通过用不同方法计算梯形ABEF的面积可验证勾股定理，请你写出验证的过程．
-
科目： 来源： 题型：
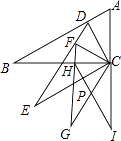
查看答案和解析>>【题目】如图，Rt△ABC中，∠B=30°，∠ACB=90°，CD⊥AB交AB于D，以CD为较短的直角边向△CDB的同侧作Rt△DEC，满足∠E=30°，∠DCE=90°，再用同样的方法作Rt△FGC，∠FCG=90°，继续用同样的方法作Rt△HIC，∠HCI=90°．若AC=a，求CI的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”，决定开设以下体育活动项目：足球、乒乓球、篮球和羽毛球，要求每位学生必须且只能选择一项，为了解选择各种体育活动项目的学生人数，随机抽取了部分学生进行调查，并将通过调查获得的数据进行整理，绘制出以下两幅不完整的统计图，请根据统计图回答问题：
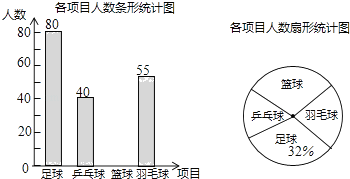
（1）这次活动一共调查了名学生；
（2）补全条形统计图；
（3）在扇形统计图中，选择篮球项目的人数所在扇形的圆心角等于度；
（4）若该学校有1500人，请你估计该学校选择足球项目的学生人数约是人． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，将一张矩形纸板按图中虚线裁剪成九块，其中有两块是边长都为
的大正方形，两块是边长都为
的小正方形，五块是长为
、宽为
的全等小矩形，且
> 
．（以上长度单位：cm）（1）观察图形，可以发现代数式
可以因式分解为 ；（2）若每块小矩形的面积为10
，四个正方形的面积和为58
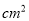，试求图中所有裁剪线（虚线部分）长之和．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，直线y=kx+1（k≠0）与双曲线y=
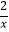（x＞0）相交于点P（1，m ）．
（1）求k的值；
（2）若点Q与点P关于直线y=x成轴对称，则点Q的坐标是Q（）；
（3）若过P、Q二点的抛物线与y轴的交点为N（0，
），求该抛物线的函数解析式，并求出抛物线的对称轴方程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某中学数学活动小组为了调查居民的用水情况，从某社区的1500户家庭中随机抽取了30户家庭的月用水量，结果如下表所示：
月用水量（吨）
3
4
5
7
8
9
10
户 数
4
3
5
11
4
2
1
（1）求这30户家庭月用水量的平均数，众数和中位数；
（2）根据上述数据，试估计该社区的月用水量；
（3）由于我国水资源缺乏，许多城市常利用分段计费的办法引导人们节约用水，即规定每个家庭的月基本用水量为m（吨），家庭月用水量不超过m（吨）的部分按原价收费，超过m吨部分加倍收费，你认为上述问题中的平均数、众数、中位数中哪一个量作为月基本用水量比较合理？简述理由。
相关试题
