【题目】如图,Rt△ABC中,∠B=30°,∠ACB=90°,CD⊥AB交AB于D,以CD为较短的直角边向△CDB的同侧作Rt△DEC,满足∠E=30°,∠DCE=90°,再用同样的方法作Rt△FGC,∠FCG=90°,继续用同样的方法作Rt△HIC,∠HCI=90°.若AC=a,求CI的长.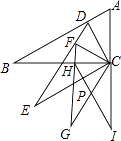
参考答案:
【答案】解:在Rt△ACB中,∠B=30°,∠ACB=90°,
∴∠A=90°﹣30°=60°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ACD=30°,
在Rt△ACD中,AC=a,
∴AD= ![]() a,
a,
由勾股定理得:CD= ![]() =
= ![]() ,
,
同理得:FC= ![]() ×
× ![]() =
= ![]() ,CH=
,CH= ![]() ×
× ![]() =
= ![]() ,
,
在Rt△HCI中,∠I=30°,
∴HI=2HC= ![]() ,
,
由勾股定理得:CI= ![]() =
= ![]() ,
,
答:CI的长为 ![]() .
.
【解析】在Rt△ACD中,利用30度角的性质和勾股定理求CD的长;同理在Rt△ECD中求FC的长,在Rt△FCG中求CH的长;最后在Rt△HCI中,利用30度角的性质和勾股定理求CI的长.
【考点精析】解答此题的关键在于理解含30度角的直角三角形的相关知识,掌握在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队修建一条长1200m的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求工程队提前2天完成任务,那么实际平均每天修建道路的工效比原计划增加百分之几? -
科目: 来源: 题型:
查看答案和解析>>【题目】一驾2.5米长的梯子靠在一座建筑物上,梯子的底部离建筑物0.7米,如果梯子的顶部滑下0.4米,梯子的底部向外滑出多远(其中梯子从AB位置滑到CD位置)?
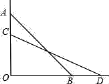
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将边长为a与b、对角线长为c的长方形纸片ABCD,绕点C顺时针旋转90°得到长方形FGCE,连接AF.通过用不同方法计算梯形ABEF的面积可验证勾股定理,请你写出验证的过程.
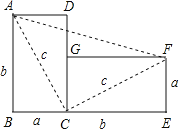
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题:
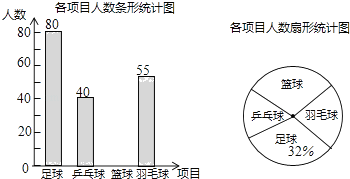
(1)这次活动一共调查了名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是人. -
科目: 来源: 题型:
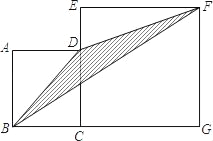
查看答案和解析>>【题目】如图,四边形ABCD和四边形EFBC均为正方形,点D在EC上.如果线段AB的长为5,则△BDF的面积为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为
 的大正方形,两块是边长都为
的大正方形,两块是边长都为 的小正方形,五块是长为
的小正方形,五块是长为 、宽为
、宽为 的全等小矩形,且
的全等小矩形,且 >
>  .(以上长度单位:cm)
.(以上长度单位:cm)(1)观察图形,可以发现代数式
 可以因式分解为 ;
可以因式分解为 ;(2)若每块小矩形的面积为10
 ,四个正方形的面积和为58
,四个正方形的面积和为58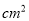 ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.
相关试题

