【题目】如图,直线AB、CD相交于点O,OM⊥AB,NO⊥CD,∠1= ![]() ∠BOC.
∠BOC.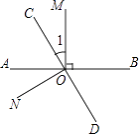
(1)求∠1的大小;
(2)求∠BON的大小.
参考答案:
【答案】
(1)解:∵OM⊥AB,
∴∠BOM=90°,
∵∠1= ![]() ∠BOC,
∠BOC,
∴∠1= ![]() ∠BOM=30°
∠BOM=30°
(2)解:∵OM⊥AB,
∴∠AOM=90°,
∵∠1=30°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∵NO⊥CD,
∴∠DON=90°,
∴∠BON=∠BOD+∠DON=150°.
【解析】(1)根据两直线垂直得出∠BOM=90°,再由∠1=![]() ∠BOC,而∠1+∠∠BOM=∠BOC,因此可推出∠1=
∠BOC,而∠1+∠∠BOM=∠BOC,因此可推出∠1=![]() ∠BOM,计算即可求出结果。
∠BOM,计算即可求出结果。
(2)先根据已知OM⊥AB,NO⊥CD,得出∠DON的度数及∠AOC或∠BOD的度数,再根据∠BON=∠BOD+∠DON,代入计算即可求出结果。
【考点精析】掌握余角和补角的特征和对顶角和邻补角是解答本题的根本,需要知道互余、互补是指两个角的数量关系,与两个角的位置无关;两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b是一个等腰三角形的两边长,且满足a2+b2-4a-6b+13=0,求这个等腰三角形的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解方程:
(1)2x2﹣x﹣15=0
(2)(2x+1)2=3(2x+1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次三项式x2-4x+3配方的结果是( )
A.(x-2)2+7
B.(x-2)2-1
C.(x+2)2+7
D.(x+2)2-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ABC=90°,AB=CB,以AB为直径的⊙O交AC于点D,点E是AB边上一点(点E不与点A、B重合),DE的延长线交⊙O于点G,DF⊥DG,且交BC于点F.

(1)求证:AE=BF;
(2)连接GB,EF,求证:GB∥EF;
(3)若AE=1,EB=2,求DG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,E、F分别在BC、AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是( )
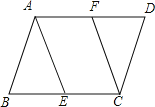
A. AF=CE B. AE=CF C. ∠BAE=∠FCD D. ∠BEA=∠FCE
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是Rt△ABC斜边AB上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于______度.

相关试题

