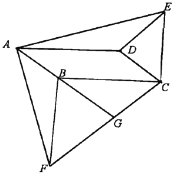
【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
参考答案:
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)证明AB=DE,FB=AD,∠ABF=∠ADE即可解决问题;
(2)只要证明FB⊥AD即可解决问题.
详(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠ABC=∠ADC,
∵BC=BF,CD=DE,
∴BF=AD,AB=DE,
∵∠ADE+∠ADC+∠EDC=360°,∠ABF+∠ABC+∠CBF=360°,∠EDC=∠CBF,
∴∠ADE=∠ABF,
在△ABF与△EDA中,
∵AB=DE,∠ABF=∠ADE,BF=AD
∴△ABF≌△EDA.
(2)证明:延长FB交AD于H.
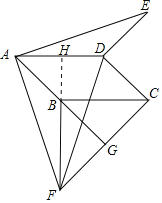
∵AE⊥AF,
∴∠EAF=90°,
∵△ABF≌△EDA,
∴∠EAD=∠AFB,
∵∠EAD+∠FAH=90°,
∴∠FAH+∠AFB=90°,
∴∠AHF=90°,即FB⊥AD,
∵AD∥BC,
∴FB⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解决问题:和、差、倍、分等问题中有着广泛的应用,截长法与补短法在证明线段的和、差、倍、分等问题中有着广泛的应用.具体的做法是在某条线段上截取一条线段等于某特定线段,或将某条线段延长,使之与某特定线段相等,再利用全等三角形的性质等有关知识来解决数学问题.
(1)如图1,在△ABC中,若 AB=12,AC=8,求 BC边上的中线AD的取值范围.
解决此问题可以用如下方法:延长AD到点E使 DE=AD,再连接 BE,把AB、AC、2AD集中在△ABE中.利用三角形三边的关系即可判断中线 AD的取值范围是_______.
问题解决:
(2)如图2,在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,CD上的两点,且∠EAF=
 ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.问题拓展:
(3)如图3,在△ABC中,∠ACB=90°,∠CAB=60°,点D是△ABC 外角平分线上一点,DE⊥AC交 CA延长线于点E,F是 AC上一点,且DF=DB.
求证:AC﹣AE=
 AF.
AF.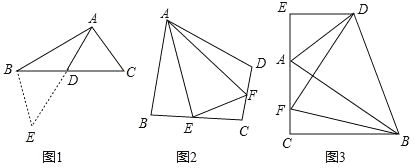
-
科目: 来源: 题型:
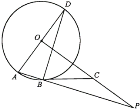
查看答案和解析>>【题目】如图,AD是⊙O的直径,AB为⊙O的弦,OP⊥AD,OP与AB的延长线交于点P,过B点的切线交OP于点C.
(1)求证:∠CBP=∠ADB.
(2)若OA=2,AB=1,求线段BP的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数y=
 (x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.
(x>0)过点A(3,4),直线AC与x轴交于点C(6,0),过点C作x轴的垂线BC交反比例函数图象于点B.(1)求k的值与B点的坐标;
(2)在平面内有点D,使得以A,B,C,D四点为顶点的四边形为平行四边形,试写出符合条件的所有D点的坐标.
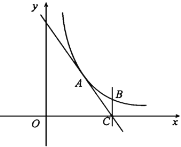
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=
 DC?请求出点C的坐标;
DC?请求出点C的坐标;(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
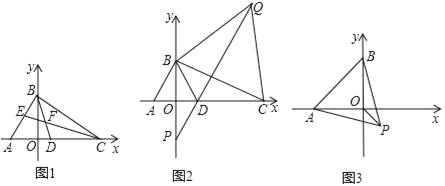
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰△ABC中,
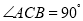 ,
,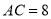 ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持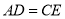 ,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)
,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)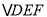 是等腰直角三角形;
是等腰直角三角形;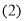 四边形CDFE不可能为正方形,(3)
四边形CDFE不可能为正方形,(3)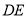 长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则
长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则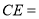
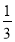 或
或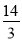 其中正确的结论个数是
其中正确的结论个数是 
A. 1个B. 2个C. 3个D. 4个
相关试题

