【题目】如图,在等腰△ABC中,![]() ,
,![]() ,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持
,F是AB边上的中点,点D、E分别在AC、BC边上运动,且保持![]() ,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)
,连接DE、DF、EF在此运动变化的过程中,下列结论:(1)![]() 是等腰直角三角形;
是等腰直角三角形;![]() 四边形CDFE不可能为正方形,(3)
四边形CDFE不可能为正方形,(3)![]() 长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则
长度的最小值为4;(4)连接CF,CF恰好把四边形CDFE的面积分成1:2两部分,则![]()
![]() 或
或![]() 其中正确的结论个数是
其中正确的结论个数是

A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】A
【解析】
连接CF,证明△ADF≌△CEF,根据全等三角形的性质判断①,根据正方形的判定定理判断②,根据勾股定理判断③,根据面积判断④.
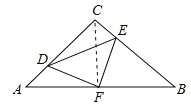
连接CF,
∵△ABC是等腰直角三角形,
∴∠FCB=∠A=![]() ,CF=AF=FB;
,CF=AF=FB;
∵AD=CE,
∴△ADF≌△CEF(SAS);
∴EF=DF,∠CFE=∠AFD;
∵∠AFD+∠CFD=90,
∴∠CFE+∠CFD=∠EFD=90,
又∵EF=DF
∴△EDF是等腰直角三角形(故(1)正确).
当D. E分别为AC、BC中点时,四边形CDFE是正方形(故(2)错误).
由于△DEF是等腰直角三角形,因此当DE最小时,DF也最小;
即当DF⊥AC时,DE最小,此时![]() .
.
∴![]() (故(3)错误).
(故(3)错误).
∵△ADF≌△CEF,
∴S△CEF=S△ADF
∴S四边形CDFE=S△AFC,
∵CF恰好把四边形CDFE的面积分成1:2两部分
∴S△CEF:S△CDF=1:2 或S△CEF:S△CDF=2:1
即S△ADF:S△CDF=1:2 或S△ADF:S△CDF=2:1
当S△ADF:S△CDF=1:2时,S△ADF=![]() S△ACF=
S△ACF=![]()
又∵S△ADF=![]()
∴2AD=![]()
∴AD=![]() (故(4)错误).
(故(4)错误).
故选:A.
-
科目: 来源: 题型:
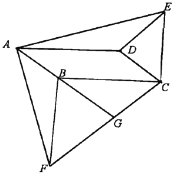
查看答案和解析>>【题目】如图,在口ABCD中,分别以边BC,CD作等腰△BCF,△CDE,使BC=BF,CD=DE,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
(2)延长AB与CF相交于G,若AF⊥AE,求证BF⊥BC.
-
科目: 来源: 题型:
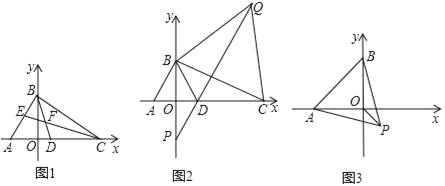
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=
 DC?请求出点C的坐标;
DC?请求出点C的坐标;(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A,B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如表所示,
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在大楼AB正前方有一斜坡CD,坡角∠DCE=30°,楼高AB=60米,在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的D处测得楼顶B的仰角为45°,其中点A,C,E在同一直线上.
(1)求坡底C点到大楼距离AC的值;
(2)求斜坡CD的长度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件__________.

相关试题

