【题目】(6分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.

(1)分别写出下列各点的坐标:A′ ; B′ ;C′ ;
(2)说明△A′B′C′由△ABC经过怎样的平移得到? .
(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(4)求△ABC的面积.
参考答案:
【答案】(1)(﹣3,1),(﹣2,﹣2),(﹣1,﹣1);(2)先向左平移4个单位,再向下平移2个单位;(3)(a﹣4,b﹣2).(4)2
【解析】
试题分析:(1)根据平面直角坐标系写出各点的坐标即可;
(2)根据对应点A、A′的变化写出平移方法即可;
(3)根据平移规律逆向写出点P′的坐标;
(4)利用△ABC所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
试题解析:1)A′(﹣3,1); B′(﹣2,﹣2);C′(﹣1,﹣1);
(2)先向左平移4个单位,再向下平移2个单位;
或:先向下平移2个单位,再向左平移4个单位;
(3)P′(a﹣4,b﹣2);
(4)△ABC的面积=2×3﹣![]() ×1×3﹣
×1×3﹣![]() ×1×1﹣
×1×1﹣![]() ×2×2
×2×2
=6﹣1.5﹣0.5﹣2
=2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)证明:∠BAE=∠FEC;
(2)证明:△AGE≌△ECF;
(3)求△AEF的面积. -
科目: 来源: 题型:
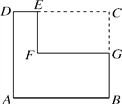
查看答案和解析>>【题目】如图,四边形ABCD是边长为4的正方形,在正方形的一个角上剪去长方形CEFG,其中E,G分别是边CD,BC上的点,且CE=3,CG=2,剩余部分是六边形ABGFED,请你建立适当的直角坐标系求六边形ABGFED各顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图一次函数y=
 x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=
x+1的图象与x轴交于点A,与y轴交于点B;二次函数y=  x2+bx+c的图象与一次函数y=
x2+bx+c的图象与一次函数y=  x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
x+1的图象交于B、C两点,与x轴交于D、E两点且D点坐标为(1,0).
(1)求二次函数的解析式;
(2)求四边形BDEC的面积S;
(3)在x轴上是否存在点P,使得△PBC是以P为直角顶点的直角三角形?若存在,求出所有的点P,若不存在,请说明理由. -
科目: 来源: 题型:
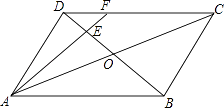
查看答案和解析>>【题目】如图,在平行四边形ABCD中,AC与BD相交于点O,E是OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
A.1:4
B.1:3
C.1:2
D.1:1 -
科目: 来源: 题型:
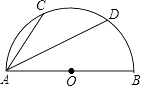
查看答案和解析>>【题目】如图,半圆O的直径AB=10cm,弦AC=6cm,AD平分∠BAC,则AD的长为( )
A.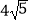 cm
cm
B.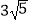 cm
cm
C.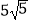 cm
cm
D.4cm -
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=
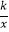 (k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( )
(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是( ) 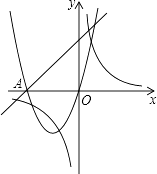
A.b=2a+k
B.a=b+k
C.a>b>0
D.a>k>0
相关试题

