Question

【题目】如图，已知图中点和点的坐标分别为和．

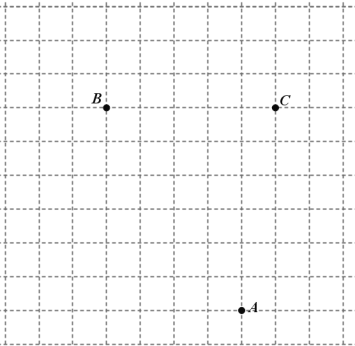
（1）请在图1中画出坐标轴建立适当的直角坐标系；

（2）写出点的坐标为________；

（3）连接、和得，在轴有点满足，则点的坐标为________，________个平方单位；

（4）已知第一象限内有两点，平移线段使点、分别落在两条坐标轴上，则点平移后的对应点的坐标是________．

Answer 1

【答案】（1）详见解析；（2）；（3）或，个平方单位；（4）或．

【解析】

(1)根据图中点和点的坐标确定原点的位置和横纵坐标的正方向即可得到答案；

(2)根据直角坐标的特点，即可写出的坐标；

(3)根据点在直角坐标系中的位置，先算出 的面积，再根据三角形的面积公式即可算出答案；

(4)根据平移后点、分别落在两条坐标轴上，得到两点横纵坐标的变化情况，分类讨论即可得到答案；

解：（1）根据图中点和点的坐标确定原点的位置和横纵坐标的正方向，得到直角坐标系如下图：

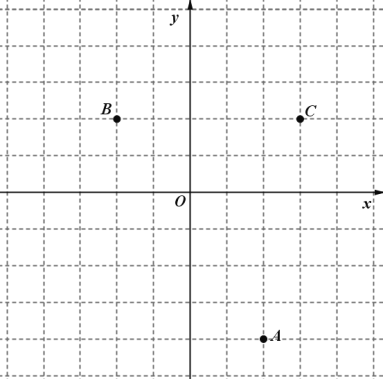
（2）根据直角坐标系的特点，得到C点的坐标为：；

（3）画图如下，

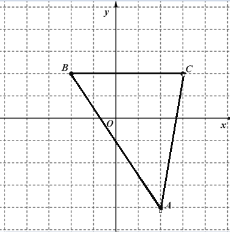
根据点在直角坐标系中的位置，得到

，

假设点的坐标为，

∴

又∵，

∴，

∴，

∴或，

故的坐标为或，个平方单位；

（4）∵第一象限的点，平移线段使点、分别落在两条坐标轴上，n＞0，

∴情况1：当平移后P点在y轴上，此时P点的横坐标为0，

则P点横坐标减少了3，

因此Q点的横坐标也减少了3，并且点Q在x轴上，

故此时Q点坐标变为，

得到Q的纵坐标,减少了n，即P点纵坐标也减少了n，

得到此时得到点平移后的对应点的坐标是；

情况2：当平移后Q点在y轴上，此时Q的横坐标为0，

则Q点横坐标减少了6个单位，

则P点的横坐标也减少了6，并且点P在x轴上，

此时P点坐标变为，

得到平移后的对应点的坐标是，

综上：点P的坐标为（0，2）或（3，0）．