【题目】如图1,E是等边三角形ABC的边AB所在直线上一点,D是边BC所在直线上一点,且D与C不重合,若EC=ED.则称D为点C关于等边三角形ABC的反称点,点E称为反称中心.
在平面直角坐标系xOy中,
(1)已知等边三角形AOC的顶点C的坐标为(2,0),点A在第一象限内,反称中心E在直线AO上,反称点D在直线OC上.
①如图2,若E为边AO的中点,在图中作出点C关于等边三角形AOC的反称点D,并直接写出点D的坐标: ;
②若AE=2,求点C关于等边三角形AOC的反称点D的坐标;
(2)若等边三角形ABC的顶点为B(n,0),C(n+1,0),反称中心E在直线AB上,反称点D在直线BC上,且2≤AE<3.请直接写出点C关于等边三角形ABC的反称点D的横坐标t的取值范围: (用含n的代数式表示).

参考答案:
【答案】(1)①D(-1,0); ②D(![]() 2,0);(2)
2,0);(2) ![]() 或
或![]()
【解析】
(1)①根据题中反称点与反称中心的定义做出点D,可得坐标;
②易得AO=OC=2,由AE=2,分E点的两个可能的位置(如图3,图4)讨论,可得D点的值;
(2)由(1)可得反称点与反称中心的规律,当B(n,0),C(n+1,0),2≤AE<3可得![]() 或
或![]() .
.
(1)① 如图,
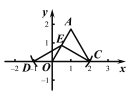 或
或 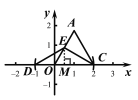
D(-1,0)
② ∵等边三角形AOC的两个顶点为O(0,0),C(2,0),
∴OC=2.
∴AO=OC=2.
由AE=2可知,点E有两个可能的位置(如图3,图4).
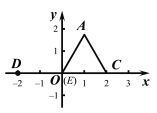

图3 图4
(ⅰ) 如图3,点E与坐标原点O重合.
∵EC=ED,EC=2,
∴ED=2.
∵D是边OC所在直线上一点,且D与C不重合,
∴D点坐标为(![]() 2,0) .
2,0) .
(ⅱ) 如图4,点E在边OA的延长线上,且AE=2.
∵AC=AE=2,
∴∠E=∠ACE.
∵△AOC为等边三角形,
∴∠OAC =∠ACO=60°.
∴∠E=∠ACE=30°.
∴∠OCE=90°.
∵EC=ED,
∴点D与点C重合.
这与题目条件中的D与C不重合矛盾,所以图4中的情况不符合要求,舍去.
综上所述:D(![]() 2,0). …
2,0). …
(2)![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠BDC,∠2+∠3=180°.
(1) 请你判断DA与CE的位置关系,并说明理由;
(2) 若DA平分∠BDC,CE⊥AE于点E,∠1=70°,试求∠FAB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知图中
 点和
点和 点的坐标分别为
点的坐标分别为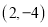 和
和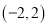 .
.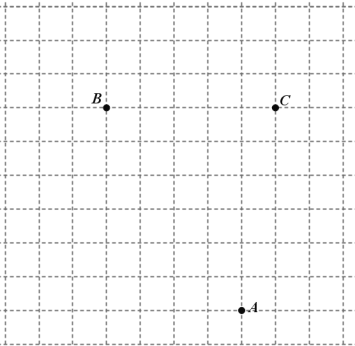
(1)请在图1中画出坐标轴建立适当的直角坐标系;
(2)写出点
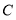 的坐标为________;
的坐标为________;(3)连接
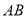 、
、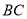 和
和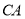 得
得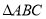 ,在
,在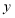 轴有点
轴有点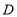 满足
满足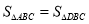 ,则点
,则点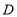 的坐标为________,
的坐标为________,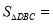 ________个平方单位;
________个平方单位;(4)已知第一象限内有两点
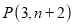 ,
,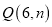 平移线段
平移线段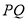 使点
使点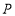 、
、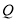 分别落在两条坐标轴上,则点
分别落在两条坐标轴上,则点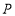 平移后的对应点的坐标是________.
平移后的对应点的坐标是________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a≠0)在平面直角坐标系中的图象,根据图形判断①c>0;②a+b+c<0;③2a﹣b<0;④b2+8a>4ac中正确的是(填写序号) .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,AC为对角线,延长CD至点E使CE=CA,连接AE。F为AB上一点,且BF=DE,连接FC.
(1)若DE=1,CF=2
 ,求CD的长。
,求CD的长。(2)如图2,点G为线段AE的中点,连接BG交AC于H,若∠BHC+∠ABG=600,求证:AF+CE=
 AC.
AC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小芸在自家楼房的窗户A处,测量楼前的一棵树CD的高.现测得树顶C处的俯角为45°,树底D处的俯角为60°,楼底到大树的距离BD为20米.请你帮助小芸计算树的高度(精确到0.1米).

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取其中32名学生两次考试考分等级制成统计图(如图),试回答下列问题:
(1)这32名学生经过培训,考分等级“不合格”的百分比由________下降到________;
(2)估计该校640名学生,培训后考分等级为“合格”与“优秀”的学生共有多少名.

相关试题

