【题目】(阅读下面材料,解答后面问题:
在数学课上,老师提出如下问题: |

小敏的作法如下:
①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=BO;③连接DA,DC.则四边形ABCD即为所求. |
判断小敏的作法是否正确?若正确,请证明;若不正确,请说明理由.
参考答案:
【答案】解:小敏的作法正确.理由如下: ∵线段AC的垂直平分线交AC于点O,
∴AO=CO,
∵BO=DO,
∴四边形ABCD为平行四边形,
∵∠ABC=90°,
∴四边形ABCD为矩形
【解析】利用基本作图得到OA=OC,OB=OD,则利用平行四边形的判定方法可判断四边形ABCD为平行四边形,然后根据矩形的判定方法得到四边形ABCD为矩形.
【考点精析】解答此题的关键在于理解矩形的判定方法的相关知识,掌握有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x+y的值是1,则代数式(x+y)2﹣x﹣y+1的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿 CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )

A.20秒
B.18秒
C.12秒
D.6秒 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列解方程中正确的有
① x+4=﹣3,解得x=﹣
x+4=﹣3,解得x=﹣ 
②3x﹣5=7x,解得x=
③﹣(x﹣1)=﹣ (x+1),解得x=3
(x+1),解得x=3
④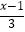 ﹣
﹣ 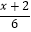 =
= 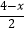 ,解得x=﹣8.
,解得x=﹣8. -
科目: 来源: 题型:
查看答案和解析>>【题目】对于抛物线y=﹣(x+1)2+3,下列结论:其中正确结论的个数为( )
①抛物线的开口向下; ②对称轴为直线x=1; ③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=x+1的图像不经过( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=-
 x+4与x轴交于点A,与y交于点C,已知二次函数的图象经过点A,C和点B(-1,0),
x+4与x轴交于点A,与y交于点C,已知二次函数的图象经过点A,C和点B(-1,0),(1)求该二次函数的关系式;
(2)设该二次函数的图象的顶点为M,求四边形AOCM的面积;
(3)有两个动点D、E同时从点O出发,其中点D以每秒
 个单位长度的速度沿折线OAC按O→A→C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O→C→A的路线运动,当点D、E两点相遇时,它们都停止运动,设D,E同时从点O出发t秒时,△ODE的面积为S,
个单位长度的速度沿折线OAC按O→A→C的路线运动,点E以每秒4个单位长度的速度沿折线OCA按O→C→A的路线运动,当点D、E两点相遇时,它们都停止运动,设D,E同时从点O出发t秒时,△ODE的面积为S,
①请问D,E两点在运动过程中,是否存在DE∥OC,若存在,请求出此时t的值,若不存在,请说明理由;
②直接写出S关于t的函数关系式,并写出自变量t的取值范围;
③在②中,当t是多少时,S有最大值,并求出这个最大值.
相关试题

