【题目】如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿 CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )
A.20秒
B.18秒
C.12秒
D.6秒
参考答案:
【答案】A
【解析】解:由题意CD=4t,AE=2t, ∵DF⊥BC于F,
∴∠DFC=90°
在Rt△DFC中,∵∠C=30°,
∴DF= ![]() CD=2t,
CD=2t,
∴DF=AE,
∵∠CFD=∠B=90°,
∴DF∥CE,
∴四边形DFEA是平行四边形,
∴当DF=AD时,四边形DFEA是菱形.
∴120﹣4t=2t,
∴t=20s,
∴t=20s时,四边形DFEA是菱形.
故选A.
【考点精析】认真审题,首先需要了解菱形的性质(菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半).
-
科目: 来源: 题型:
查看答案和解析>>【题目】现定义两种运算“⊕”“*”.对于任意两个整数,a⊕b=a+b-1,a*b=a×b-1,则(6⊕8)*(3⊕5)的结果是( )
A. 60 B. 90 C. 112 D. 69
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC.
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE= 时,四边形BFCE是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若代数式x+y的值是1,则代数式(x+y)2﹣x﹣y+1的值是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列解方程中正确的有
① x+4=﹣3,解得x=﹣
x+4=﹣3,解得x=﹣ 
②3x﹣5=7x,解得x=
③﹣(x﹣1)=﹣ (x+1),解得x=3
(x+1),解得x=3
④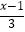 ﹣
﹣ 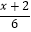 =
= 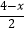 ,解得x=﹣8.
,解得x=﹣8. -
科目: 来源: 题型:
查看答案和解析>>【题目】(阅读下面材料,解答后面问题:
在数学课上,老师提出如下问题:
已知:Rt△ABC,∠ABC=90°
求作:矩形ABCD.
小敏的作法如下:①作线段AC的垂直平分线交AC于点O;②连接BO并延长,在延长线上截取OD=BO;③连接DA,DC.则四边形ABCD即为所求.
判断小敏的作法是否正确?若正确,请证明;若不正确,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于抛物线y=﹣(x+1)2+3,下列结论:其中正确结论的个数为( )
①抛物线的开口向下; ②对称轴为直线x=1; ③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小
A. 1B. 2C. 3D. 4
相关试题

