【题目】如图, 已知BE平分∠ABD, DE平分∠BDC, 并且∠1+∠3=90°, 则__∥___理由是____________.

参考答案:
【答案】CD AB 同旁内角互补,两直线平行
【解析】
由角平分线的性质可得出得出∠BDC=2∠1、∠ABD=2∠3,结合∠1+∠3=90°可得出∠BDC+∠ABD=180°,利用“同旁内角互补,两直线平行”即可证出AB∥CD.
证明:∵DE平分∠BDC(已知),
∴∠BDC=2∠1(角平分线的性质).
∵BE平分∠ABD(已知),
∴∠ABD=2∠3(角平分线的性质).
∴∠BDC+∠ABD=2∠1+2∠3=2(∠1+∠3)(等量代换).
∵∠1+∠3=90°(已知),
∴∠BDC+∠ABD=180°(等量代换).
∴AB∥CD(同旁内角互补,两直线平行).
故答案为:CD;AB;同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠C=90 o,AC=BC=4,点D是AB的中点,E.F在射线AC与射线CB上运动,且满足AE=CF;当点E运动到与点C的距离为1时,则△DEF的面积为___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察、猜想、探究:
在
 中,
中, .
. 如图
如图 ,当
,当 ,AD为
,AD为 的角平分线时,求证:
的角平分线时,求证: ;
; 如图
如图 ,当
,当 ,AD为
,AD为 的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;
的角平分线时,线段AB、AC、CD又有怎样的数量关系?不需要证明,请直接写出你的猜想;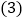 如图
如图 ,当AD为
,当AD为 的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
的外角平分线时,线段AB、AC、CD又有怎样的数量关系?请写出你的猜想,并对你的猜想给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ,
, ,E是AB上的一点,且
,E是AB上的一点,且 ,
, .
. 求证:
求证: ≌
≌ ;
; 若
若 ,
, ,请求出CD的长.
,请求出CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
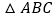 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点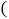 点D不与B,C重合
点D不与B,C重合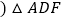 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF. 如图1,求证:
如图1,求证: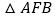 ≌
≌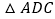 ;
; 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;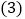 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问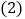 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,∠AEC等于( )

A.56° B.66° C.76° D.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)在△BED中作BD边上的高,垂足为F;
(2)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?

相关试题

