搜索
【题目】观察、猜想、探究：
在
中，
．
如图
，当
，AD为
的角平分线时，求证：
；
如图
，当
，AD为的角平分线时，线段AB、AC、CD又有怎样的数量关系？不需要证明，请直接写出你的猜想；
如图
，当AD为的外角平分线时，线段AB、AC、CD又有怎样的数量关系？请写出你的猜想，并对你的猜想给予证明．
参考答案：
【答案】(1)见解析;(2) AB=CD+AC ,理由见解析;(3) B=CD-AC,理由见解析.
【解析】
(1)过D作DE⊥AB，交AB于点E，理由角平分线性质得到ED=CD，利用HL得到直角三角形AED与直角三角形ACD全等，由全等三角形的对应边相等，对应角相等，得到AE=AC，∠AED=∠ACB，由∠ACB=2∠B，利用等量代换及外角性质得到一对角相等，利用等角对等边得到BE=DE，由AB=AE+EB，等量代换即可得证；
(2)AB=CD+AC，理由为：在AB上截取AG=AC，如图2所示，由角平分线定义得到一对角相等，再由AD=AD，利用SAS得到三角形AGD与三角形ACD全等，接下来同(1)即可得证；
(3)AB=CD-AC，理由为：在AF上截取AG=AC，如图3所示，同(2)即可得证．
过D作
，交AB于点E，如图1所示，
为
的平分线，
，，
，
在
和
中，
，
≌
，
，
，
，
，
又
，
，
，
则
；
，理由为：
在AB上截取
，如图2所示，
为的平分线，
，
在
和
中，
，
≌
，
，
，
，
，
又
，
，
，
则
；
，理由为：
在AF上截取，如图3所示，
为
的平分线，
，
在和
中，
，
≌
，
，
，即
，
，
，
又
，
，
.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ=PQ，PR=PS，下面四个结论：①AS=AR；②QP∥AR；③△BRP≌△QSP；④AP垂直平分RS．其中正确结论的序号是 （请将所有正确结论的序号都填上）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一次函数y=x+b的图象与反比例函数y=
（k为常数，k≠0）的图象交于点A（﹣1，4）和点B（a，1）． 
（1）求反比例函数的表达式和a、b的值；
（2）若A、O两点关于直线l对称，请连接AO，并求出直线l与线段AO的交点坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图,在等腰直角三角形ABC中,∠C=90 o，AC=BC=4，点D是AB的中点，E.F在射线AC与射线CB上运动，且满足AE=CF；当点E运动到与点C的距离为1时，则△DEF的面积为___________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，
，E是AB上的一点，且
，
．
求证：
≌
；
若
，
，请求出CD的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图, 已知BE平分∠ABD, DE平分∠BDC, 并且∠1＋∠3＝90°, 则__∥___理由是____________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
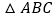是等边三角形，D是BC边上的一个动点
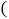点D不与B，C重合
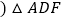是以AD为边的等边三角形，过点F作BC的平行线交射线AC于点E，连接BF．
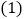如图1，求证：
≌
；
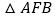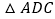请判断图1中四边形BCEF的形状，并说明理由；
若D点在BC边的延长线上，如图2，其它条件不变，请问中结论还成立吗？如果成立，请说明理由．
相关试题
