【题目】如图是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图.
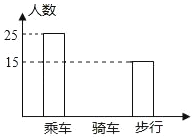
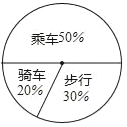
(1)求该班有多少名学生?
(2)补上骑车分布直方图的空缺部分;
(3)在扇形统计图中,求步行人数所占的圆心角度数;
(4)若全年级有900人,估计该年级骑车人数.
参考答案:
【答案】(1)50人;(2)补全图形见解析(3)108°;(4)估计该年级骑车人数为180.
【解析】分析:(1)由乘车的人数除以占的百分比求出该班的学生数即可;
(2)由该班的人数求出骑车的学生数,补全条形统计图即可;
(3)根据步行占的百分比,乘以360即可得到结果;
(4)由骑车的百分比乘以900即可得到结果.
详解:(1)该班的学生总数为25÷50%=50人;
(2)骑车的人数为50×20%=10,
补全图形如下:
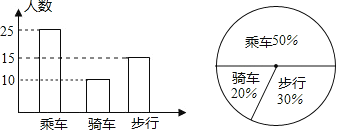
(3)步行人数所占的圆心角度数为360°×30%=108°;
(4)900×20%=180,
答:估计该年级骑车人数为180.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:
 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:设
 (其中
(其中 均为整数),则有
均为整数),则有  .
.∴
 .这样小明就找到了一种把部分
.这样小明就找到了一种把部分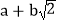 的式子化为平方式的方法.
的式子化为平方式的方法.请你仿照小明的方法探索并解决下列问题:
(1)当
 均为正整数时,若
均为正整数时,若 ,用含m、n的式子分别表示
,用含m、n的式子分别表示 ,得
,得  = ,
= , = ;
= ;(2)利用所探索的结论,找一组正整数
 ,填空: +
,填空: +  =( +
=( +  )2;
)2;(3)若
 ,且
,且 均为正整数,求
均为正整数,求 的值.
的值.【答案】(1)
 ;
; ;(2)4,2,1,1(答案不唯一);(3)
;(2)4,2,1,1(答案不唯一);(3) =7或13
=7或13【解析】分析:(1)由a+b
 =(m+n
=(m+n )2,展开比较系数可得答案;
)2,展开比较系数可得答案;(2)取m=1,n=1,可得a和b的值,可得答案;
(3)由题意得m和n的方程,解方程可得m和n,可得a值.
详解:(1)∵a+b
 =(m+n
=(m+n )2,
)2,∴a+b
 =m2+3n2+2mn
=m2+3n2+2mn ,
,∴a=m2+3n2,b=2mn.
故答案为:m2+3n2,2mn.
(2)设m=1,n=1,
∴a=m2+3n2=4,b=2mn=2.
故答案为4、2、1、1.
(3)由题意,得:
a=m2+3n2,b=2mn
∵4=2mn,且m、n为正整数,
∴m=2,n=1或者m=1,n=2,
∴a=22+3×12=7,或a=12+3×22=13.
点睛:本题主要考查二次根式的混合运算,完全平方公式,解题的关键在于熟练运算完全平方公式和二次根式的运算法则.
【题型】解答题
【结束】
28【题目】如图1,已知点A(a,0),B(0,b),且a、b满足
 ,
,□ABCD的边AD与y轴交于点E,且E为AD中点,双曲线
 经过C、D两点.
经过C、D两点.(1)若点D点纵坐标为t,则C点纵坐标为 (含t的代数式表示),k的值为 ;
(2)点P在双曲线
 上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;
上,点Q在y轴上,若以点A、B、P、Q为顶点的四边形是平行四边形,试求满足要求的所有点P、Q的坐标;(3)以线段AB为对角线作正方形AFBH(如图3),点T是边AF上一动点,M是HT的中点,MN⊥HT,交AB于N,连接FN,当T在AF上运动时,试判断∠ATH与∠AFN之间的数量关系,并说明理由。


-
科目: 来源: 题型:
查看答案和解析>>【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,﹣4),画出平移后对应的△A2B2C2;
(2)在x轴上有一点P,使得PA+PB的值最小,请求出点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)2(10﹣0.5y)=﹣(1.5y+2)
(2)
 (x﹣5)=3﹣
(x﹣5)=3﹣ (x﹣5)
(x﹣5)(3)
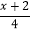 ﹣1=
﹣1=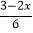
(4)x﹣
 (x﹣9)=
(x﹣9)= [x+
[x+ (x﹣9)]
(x﹣9)](5)
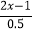 -
- =0.5x+2
=0.5x+2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有20个球,其中红球6个,白球和黑球若干个,每个球除颜色外完全相同.
(1)小明通过大量重复试验(每次将球搅匀后,任意摸出一个球,记下颜色后放回)发现,摸出的黑球的频率在0.4附近摆动,请你估计袋中黑球的个数.
(2)若小明摸出的第一个球是白球,不放回,从袋中余下的球中再任意摸出一个球,摸出白球的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人想共同承包一项工程,甲单独做30天完成,乙单独做20天完成,合同规定15天完成,若完不成视为违约,甲乙两人经过商量后签订了该合同.
(1)正常情况下,甲乙两人能否履行该合同?为什么?
(2)现在两人合作了9天,因别处有急事,必需调走1人,问两人能否违约?
相关试题

