【题目】快车和慢车分别从甲、乙两地同时出发,匀速相向而行,快车到达乙地后,慢车继续前行,设出发![]() 小时后,两车相距
小时后,两车相距![]() 千米,图中折线表示从两车出发至慢车到达甲地的过程中
千米,图中折线表示从两车出发至慢车到达甲地的过程中![]() 与
与![]() 之间的函数关系式,根据图中信息,解答下列问题.
之间的函数关系式,根据图中信息,解答下列问题.
(1)甲、乙两地相距 千米,快车从甲地到乙地所用的时间是 小时;
(2)求线段![]() 的函数解析式(写出自变量取值范围),并说明点
的函数解析式(写出自变量取值范围),并说明点![]() 的实际意义.
的实际意义.
(3)求快车和慢车的速度.

参考答案:
【答案】(1)640,6.4;(2)y=-160x+640,自变量取值范围是0≤x≤4,Q点为快车与慢车相遇的时间;(3)快车速度:100千米/时;慢车速度:60千米/时.
【解析】
PQ段的速度表示两车速度和,在Q点表示两车相遇,M点表示快车已经到达了乙地,MN表示只有慢车还在行驶
(1)直接由图像即可得到结果 (2)利用P点和(![]() ,440)可求出直线PQ的解析式,然后求出Q点,自变量的取值范围即从0到Q的横坐标 (3)由PQ直线算出速度和,由第一问得到快车的速度,然后得到慢车速度即可
,440)可求出直线PQ的解析式,然后求出Q点,自变量的取值范围即从0到Q的横坐标 (3)由PQ直线算出速度和,由第一问得到快车的速度,然后得到慢车速度即可
(1)由图像可知,两车未出发时两车最远,即甲乙两地的距离为640km;由图像可知在6.4小时之后只有慢车还在运动,所以快车从甲地到达乙地的时间为6.4小时
(2)因为P点坐标为(0,640),所以可设PQ直线解析式为y=kx+640,将点(![]() ,440)代入,得到方程440=
,440)代入,得到方程440=![]() k+640,解得k=-160,所以PQ函数解析式为y=-160x+640;Q点的坐标为(4,0),所以线段PQ函数解析式的自变量取值范围是0≤x≤4,Q点的意义是快车与慢车相遇的时间
k+640,解得k=-160,所以PQ函数解析式为y=-160x+640;Q点的坐标为(4,0),所以线段PQ函数解析式的自变量取值范围是0≤x≤4,Q点的意义是快车与慢车相遇的时间
(3)由PQ段可得到两车的速度和为(640-440)÷![]() =160km/h,由(1)可得到快车的速度为640÷6.4=100km/h,则慢车速度为60km/h
=160km/h,由(1)可得到快车的速度为640÷6.4=100km/h,则慢车速度为60km/h
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,BI,CI分别平分∠ABC,∠ACB,过I点作DE∥BC,交AB于D,交AC于E,给出下列结论:①△DBI是等腰三角形;②△ACI是等腰三角形;③AI平分∠BAC;④△ADE周长等于AB+AC.其中正确的是( )

A. ①②③ B. ②③④ C. ①③④ D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是( )
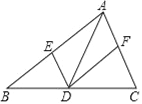
A. 若AD⊥BC,则四边形AEDF是矩形
B. 若AD垂直平分BC,则四边形AEDF是矩形
C. 若BD=CD,则四边形AEDF是菱形
D. 若AD平分∠BAC,则四边形AEDF是菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学老师布置了一道思考题“计算:(-
 )÷(
)÷(
 )”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.
)”,小明仔细思考了一番,用了一种不同的方法解决了这个问题.小明的解法:原式的倒数为(

 )÷(
)÷( )=(
)=(
 )×(-12)=-4+10=6,所以(-
)×(-12)=-4+10=6,所以(- )÷(
)÷(
 )=
)= .
.(1)请你判断小明的解答是否正确,并说明理由.
(2)请你运用小明的解法解答下面的问题.
计算:(-
 )÷(
)÷(
 +
+ ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上,我们把表示数2的点定为核点,记作点
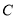 ,对于两个不同的点
,对于两个不同的点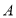 和
和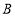 ,若点
,若点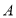 ,
,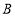 到点
到点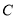 的距离相等,则称点
的距离相等,则称点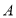 与点
与点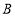 互为核等距点.如图,点
互为核等距点.如图,点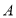 表示数-1,点
表示数-1,点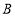 表示数5,它们与核点
表示数5,它们与核点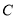 的距离都是3个单位长度,我们称点
的距离都是3个单位长度,我们称点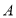 与点
与点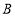 互为核等距点.
互为核等距点.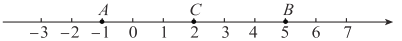
(1)已知点
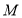 表示数3,如果点
表示数3,如果点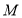 与点
与点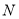 互为核等距点,那么点
互为核等距点,那么点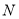 表示的数是______;
表示的数是______;(2)已知点
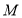 表示数
表示数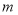 ,点
,点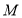 与点
与点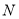 互为核等距点,
互为核等距点,①如果点
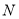 表示数
表示数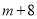 ,求
,求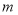 的值;
的值;②对点
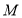 进行如下操作:先把点
进行如下操作:先把点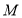 表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点
表示的数乘以2,再把所得数表示的点沿着数轴向左移动5个单位长度得到点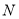 ,求
,求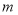 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】点A、B在数轴上的位置如图所示:

(1)点A表示的数是 ,点B表示的数是 ;
(2)在原图中分别标出表示+1.5的点C、表示﹣3.5的点D;
(3)在上述条件下,B、C两点间的距离是 ,A、C两点间的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一牧童在A处牧马,牧童家在B处,A、B距河岸的距离AC、BD的长分别为500米和700米,且C、D两地的距离为1600米,天黑前牧童从A点将马牵引到河边去饮水后再赶回家,那么牧童至少要走的距离是( )
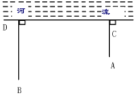
A. 2600米B. 2300米C. 2000米D. 1200米
相关试题

