【题目】为召开球类运动会,学校决定购买一批篮球和足球,若购买3个篮球和2个足球共需420元;购买2个篮球和4个足球共需440元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中购买篮球的数量不少于足球数量的![]() ,学校可用于购买这批篮球和足球的资金最多为8000元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为8000元.请问有几种购买方案?
(3)若购买篮球![]() 个,学校购买这批篮球和足球的总费用为
个,学校购买这批篮球和足球的总费用为![]() 元,在(2)的条件下,求哪种方案能使
元,在(2)的条件下,求哪种方案能使![]() 最小,并求出
最小,并求出![]() 的最小值.
的最小值.
参考答案:
【答案】(1)篮球单价为100元,足球单价为60元;(2)有11种购买方案.;(3)见解析,![]() 最小为7600元.
最小为7600元.
【解析】
(1)设每个篮球x元,每个足球y元,构建方程组即可解决问题;
(2)设购买篮球m个,足球(100-m)个,构建不等式组,求整数解即可;
(3)构建一次函数,利用一次函数的性质即可解决问题.
(1)设每个篮球x元,每个足球y元,由题意,得:
![]()
解得![]()
答:篮球单价为100元,足球单价为60元.
(2)设购买篮球m个,足球(100-m)个,由题意可得:
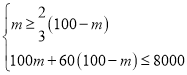
解得:40≤m≤50,
∵m为正整数,
∴m=40,41,42,43,44,45,46,47,48,49,50,
∴共有11种购买方案.
(3)由题意可得y=100x+60(100-x)=40x+6000(40≤x≤50)
∵k=40>0
∴y随x的增大而增大
∴当x=40时,y有最小值,y最小=40×40+6000=7600(元)
所以当x=40时,y的最小值为7600元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx-2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=-2和x=5时二次函数的函数值y相等.

(1)求实数a,b的值;
(2)如图①,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒
 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由;
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解八年级学生对
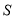 (科学)、
(科学)、 (技术)、
(技术)、 (工程)、
(工程)、 (艺术)、
(艺术)、 (数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(1)这次抽样调查共调查了多少名学生?
(2)补全条形统计图;
(3)求扇形统计图中
 (数学)所对应的圆心角度数;
(数学)所对应的圆心角度数;(4)若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对
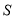 (科学)最感兴趣的学生大约有多少人?
(科学)最感兴趣的学生大约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )

A. 65°B. 60°C. 50°D. 40°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则小聪行走的路程为 m.

-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)9x2-100=0 (2)x(x-1)=2(x-1)
(3)(x+2)(x+3)=20 (4)3x2-4x-1=0
相关试题

