【题目】某校为了了解八年级学生对![]() (科学)、
(科学)、![]() (技术)、
(技术)、![]() (工程)、
(工程)、![]() (艺术)、
(艺术)、![]() (数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:

(1)这次抽样调查共调查了多少名学生?
(2)补全条形统计图;
(3)求扇形统计图中![]() (数学)所对应的圆心角度数;
(数学)所对应的圆心角度数;
(4)若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对![]() (科学)最感兴趣的学生大约有多少人?
(科学)最感兴趣的学生大约有多少人?
参考答案:
【答案】(1)50;(2)见解析;(2)![]() ;(3)144人.
;(3)144人.
【解析】
(1)根据S(科学),的人数除以百分比,计算即可;
(2)求出A组人数,画出条形图即可;
(3)根据圆心角=360°×百分比计算即可;
(4)利用样本估计总体的思想解决问题即可;
(1)18÷36%=50(人),
答:这次抽样调查共调查了50名学生.
(2)A组人数=50-18-4-3-10=15,
条形图如图所示:
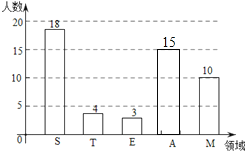
(3)10÷50×100%=20%,
360°×20%=72°,
答:扇形统计图中M(数学)所对应的圆心角度数为72°.
(4)400×36%=144(人),
答:根据样本数据估计该校八年级学生中对S(科学)最感兴趣的学生大约有144人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图点P是△ABC的边BC上的一动点,点E与点P关于直线AB成轴对称,连接EP交AB于点F,连接AP、EC相交于点O,连接AE.

(1)判断AE与AP的数量关系,并说明理由.
(2)在点P的运动过程中,当AE∥BC时,判断AP与BP的数量关系,并说明理由.
(3)若∠BAC=900,点P在运动过程中是否存在线段AP与线段EC互相平分的情况,若存在,请求出点P的位置;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连结DF、CF.

(1)如图1, 当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC=
 ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx-2的图象与x轴交于A,B两点,与y轴交于点C,点A的坐标为(4,0),且当x=-2和x=5时二次函数的函数值y相等.

(1)求实数a,b的值;
(2)如图①,动点E,F同时从A点出发,其中点E以每秒2个单位长度的速度沿AB边向终点B运动,点F以每秒
 个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.
个单位长度的速度沿射线AC方向运动.当点E停止运动时,点F随之停止运动.设运动时间为t秒.连接EF,将△AEF沿EF翻折,使点A落在点D处,得到△DEF.①是否存在某一时刻t,使得△DCF为直角三角形?若存在,求出t的值;若不存在,请说明理由;
②设△DEF与△ABC重叠部分的面积为S,求S关于t的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD

(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABCD?若存在,求点P坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为召开球类运动会,学校决定购买一批篮球和足球,若购买3个篮球和2个足球共需420元;购买2个篮球和4个足球共需440元.
(1)求篮球和足球的单价;
(2)根据实际需要,学校决定购买篮球和足球共100个,其中购买篮球的数量不少于足球数量的
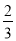 ,学校可用于购买这批篮球和足球的资金最多为8000元.请问有几种购买方案?
,学校可用于购买这批篮球和足球的资金最多为8000元.请问有几种购买方案?(3)若购买篮球
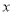 个,学校购买这批篮球和足球的总费用为
个,学校购买这批篮球和足球的总费用为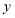 元,在(2)的条件下,求哪种方案能使
元,在(2)的条件下,求哪种方案能使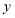 最小,并求出
最小,并求出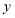 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,∠ABC=25°,以点C为旋转中心顺时针旋转后得到△A′B′C,且点A在边A′B′上,则旋转角的度数为( )

A. 65°B. 60°C. 50°D. 40°
相关试题

