Question

【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则小聪行走的路程为 　 m.

Answer 1

【答案】4600.

【解析】小敏走的路程为AB+AG+GE=1500+（AG+GE）=3100，则AG+GE=1600m，

小聪走的路程为BA+AD+DE+EF=3000+（DE+EF）.

连接CG，

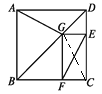
在正方形ABCD中，∠ADG=∠CDG=45°，AD=CD，

在△ADG和△CDG中，

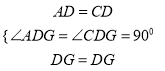
∴△ADG△CDG，

∴AG=CG.

又∵GE⊥CD，GF⊥BC，∠BCD=90°，

∴四边形GECF是矩形，

∴CG=EF.

又∵∠CDG=45°，

∴DE=GE，

∴小聪走的路程为BA+AD+DE+EF=3000+（GE+AG）=3000+1600=4600m.