【题目】如图,已知A(0,a),B(0,b),C(m,b)且(a-4)2+![]() =0,
=0,![]()
(1)求C点坐标
(2)作DE DC,交y轴于E点,EF为 AED的平分线,且DFE= 90o。 求证:FD平分ADO;
(3)E 在 y 轴负半轴上运动时,连 EC,点 P 为 AC 延长线上一点,EM 平分∠AEC,且 PM⊥EM,PN⊥x 轴于 N 点,PQ 平分∠APN,交 x 轴于 Q 点,则 E 在运动过程中,![]() 的大小是否发生变化,若不变,求出其值.
的大小是否发生变化,若不变,求出其值.


参考答案:
【答案】(1)![]() ;(2)详解见解析;(3)
;(2)详解见解析;(3)![]() 的大小不发生变化,理由见解析
的大小不发生变化,理由见解析
【解析】
(1)首先求出a,b,根据A,B两点坐标以及△ABC的面积即可计算得到C点坐标;
(2)利用角平分线以及直角三角形的性质进行角之间的转化即可证明FD平分![]() ;
;
(3)利用平行得到![]() ,
,![]() ,再利用三角形内角和、直角三角形与角平分线的性质将
,再利用三角形内角和、直角三角形与角平分线的性质将![]() ,
,![]() 用
用![]() ,
,![]() 表示即可得到
表示即可得到![]() 的值.
的值.
(1)![]()
![]() ,且
,且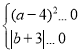 ,
,
∴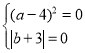 ,解得
,解得![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
又![]()
![]() 的面积是14,
的面积是14,
∴![]() ,
,
解得![]()
∴![]() 点坐标为
点坐标为![]() ;
;
(2)设EF与x轴交于点H,
![]()
![]() ,
,
∴![]() ,
,
又![]()
![]() ,且
,且![]() ,
,
∴![]() ,
,
![]()
![]() ,
,
∴![]() ,
,
![]()
![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]()
![]() 为
为![]() 的平分线,
的平分线,
∴![]() ,
,
∴![]() ,即
,即![]() 平分
平分![]() ;
;
(3)![]() 的大小不发生变化,其值为
的大小不发生变化,其值为![]() ,理由如下,
,理由如下,
如图所示,延长![]() 交y轴于点
交y轴于点![]()
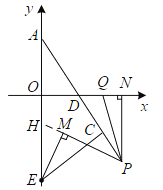
由题意可得![]() ,
,
∴![]() ,
,![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ,
,
又![]()
![]() ,
,
∴![]() ,
,
又![]()
![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 的大小不发生变化,为
的大小不发生变化,为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,二次函数y=x2+mx+2m﹣7的图象经过点(1,0).
(1)求抛物线的表达式;
(2)把﹣4<x<1时的函数图象记为H,求此时函数y的取值范围;
(3)在(2)的条件下,将图象H在x轴下方的部分沿x轴翻折,图象H的其余部分保持不变,得到一个新图象M.若直线y=x+b与图象M有三个公共点,求b的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在平面直角坐标系中,点A(0,3),点B(﹣3,0),点C(1,0),点D(0,1),连AB,AC,BD.
(1)求证:BD⊥AC;
(2)如图②,将△BOD绕着点O旋转,得到△B′OD′,当点D′落在AC上时,求AB′的长;
(3)试直接写出(Ⅱ)中点B′的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数
 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:① ;②
;② ;③
;③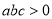 ;④
;④ ;⑤
;⑤ 其中所有正确结论的序号是( )
其中所有正确结论的序号是( )
A. ①② B. ①③④ C. ①②③⑤ D. ①②③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图,则一次函数y=bx+b2﹣4ac与反比例函数y=
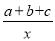 在同一坐标系内的图象大致为( )
在同一坐标系内的图象大致为( )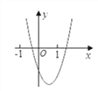
A.
 B.
B.  C.
C. 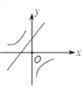 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用一张高为30
 ,宽为
,宽为 的长方形打印纸打印文档,如果左右的页边距都为
的长方形打印纸打印文档,如果左右的页边距都为 ,上下页边距比左右页边距多
,上下页边距比左右页边距多 .
.(1)请用
 的代数式表示中间打印部分的面积.
的代数式表示中间打印部分的面积.(2)当
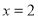 时,中间打印部分的面积是多少平方厘米?
时,中间打印部分的面积是多少平方厘米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料一:小明计算
 ,发现其结果为
,发现其结果为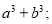 计算
计算 ,发现其结果为
,发现其结果为
阅读材料二:小华发现一个有趣的算式

(1)请模仿小华的算式,再写出一个类似的正确算式;
(2)请用字母表示小华算式的规律;
(3)请用阅读材料一中蕴含的数学规律或你掌握的数学知识说明(2)中的规律为何成立.
相关试题

