【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,CE⊥CD且CE=CD,连接EF. 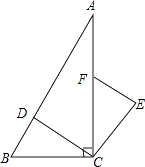
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
参考答案:
【答案】
(1)证明:∵∠ACB=90°,CE⊥CD,
∴∠BCD+∠DCA=90°=∠DCA+∠FCE,
∴∠BCD=∠FCE.
在△BCD和△FCE中, 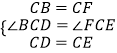 ,
,
∴△BCD≌△FCE(SAS)
(2)解:∵△BCD≌△FCE,
∴∠BDC=∠FEC.
∵EF∥CD,
∴∠DCE+∠FEC=180°,
又∵CE⊥CD,
∴∠FEC=180°﹣∠DCE=180°﹣90°=90°,
∴∠BDC=90°
【解析】(1)根据∠ACB=90°、CE⊥CD利用角的计算即可得出∠BCD=∠FCE,再结合CB=CF、CD=CE即可证出△BCD≌△FCE(SAS);(2)由(1)可得出∠BDC=∠FEC,由EF∥CD利用平行线的性质即可得出∠DCE+∠FEC=180°,再结合CE⊥CD即可得出结论.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校在“爱护地球,绿化祖国”的创建活动中,组织学生开展植树造林活动.为了解全校学生的植树情况,学校随机抽查了100名学生的植树情况,将调查数据整理如下表:
则这100名同学平均每人植树_____棵;若该校共有1000名学生,请根据以上调查结果估计该校学生的植树总数是______棵.
植树数量(单位:棵)
4
5
6
8
10
人数
28
20
25
16
11
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程 x2= x的根是( )
A. x1=0,x2=1 B. x1=0,x2=-1 C. x1=x2=0 D. x1=x2=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a2?a3=a6
B.(﹣2xy2)3=﹣8x3y5
C.2a﹣3=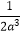
D.(﹣a)3÷(2a)2=﹣ a
a -
科目: 来源: 题型:
查看答案和解析>>【题目】某公司经过市场调查发现,该公司生产的某商品在第x天的售价(1≤x≤42)为(x+40)元/件,而该商品每天的销量满足关系式y=200-2x.如果该商品第20天的售价按7折出售,仍然可以获得40%的利润
(1) 求该公司生产每件商品的成本为多少元
(2) 问销售该商品第几天时,每天的利润最大?最大利润是多少?
(3) 试计算公司共有多少天利润不低于3600元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P在第二象限,且到两条坐标轴的距离都是4,则点P的坐标为( )
A. (﹣4,4) B. (﹣4,﹣4) C. (4,﹣4) D. (4,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的标价为120元,若以九折降价出售,相对于进价仍获得20%,则该商品的进价是( )
A.95元
B.90元
C.85元
D.80元
相关试题

