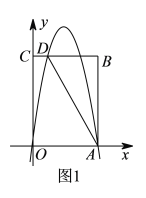
【题目】如图![]() ,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交BC于点D.tan∠OAD=2,抛物线
,矩形OABC的顶点A,C的坐标分别为(4,0),(0,6),直线AD交BC于点D.tan∠OAD=2,抛物线![]() 过A,D两点.
过A,D两点.
(![]() )求点D的坐标和抛物线M1的表达式.
)求点D的坐标和抛物线M1的表达式.
(![]() )点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有满足条件的点P的坐标.
)点P是抛物线M1对称轴上一动点,当∠CPA=90°时,求所有满足条件的点P的坐标.
(![]() )如图
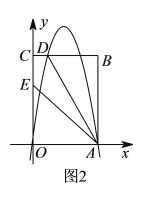
)如图![]() ,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.
,点E(0,4),连接AE,将抛物线M1的图象向下平移m(m>0)个单位得到抛物线M2.
①设点D平移后的对应点为点D',当点D'恰好落在直线AE上时,求m的值.
②当![]() 时,若抛物线M2与直线AE有两个交点,求m的取值范围.
时,若抛物线M2与直线AE有两个交点,求m的取值范围.
参考答案:
【答案】(1)D(1,6),抛物线M1的表达式为y=﹣2x2+8x;(2)(2,3+![]() ),(2,3﹣
),(2,3﹣![]() );(3)①m=3,②2+
);(3)①m=3,②2+![]() ≤m<
≤m<![]()
【解析】
(1)如图1中,作DH⊥OA于H.则四边形CDHO是矩形.在Rt△ADH中,解直角三角形,求出点D坐标,利用待定系数法即可解决问题;
(2)如图1﹣1中,设P(2,m).由∠CPA=90°,可得PC2+PA2=AC2,可得22+(m﹣6)2+22+m2=42+62,解方程即可;
(3)①求出D′的坐标;②构建方程组,利用判别式△>0,求出抛物线与直线AE有两个交点时的m的范围;③求出x=m时,求出平移后的抛物线与直线AE的交点的横坐标;结合上述的结论即可判断.
解:(1)如图1中,作DH⊥OA于H.则四边形CDHO是矩形.
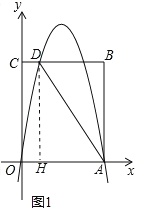
∵四边形CDHO是矩形,
∴OC=DH=6,
∵tan∠DAH=![]() =2,
=2,
∴AH=3,
∵OA=4,
∴CD=OH=1,
∴D(1,6),
把D(1,6),A(4,0)代入y=ax2+bx中,则有![]() ,
,
解得![]() ,
,
∴抛物线M1的表达式为y=﹣2x2+8x.
(2)如图1﹣1中,设P(2,m).
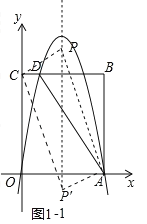
∵∠CPA=90°,
∴PC2+PA2=AC2,
∴22+(m﹣6)2+22+m2=42+62,
解得m=3±![]() ,
,
∴P(2,3+![]() ),P′(2,3﹣
),P′(2,3﹣![]() ).
).
(3)①如图2中,

易知直线AE的解析式为y=﹣x+4,
x=1时,y=3,
∴D′(1,3),
平移后的抛物线的解析式为y=﹣2x2+8x﹣m,
把点D′坐标代入可得3=﹣2+8﹣m,
∴m=3.
②由![]() ,消去y得到2x2﹣9x+4+m=0,
,消去y得到2x2﹣9x+4+m=0,
当抛物线与直线AE有两个交点时,△>0,
∴92﹣4×2×(4+m)>0,
∴m<![]() ,
,
当x=m时,﹣m+4=﹣2m2+8m﹣m,解得m=2+![]() 或2﹣
或2﹣![]() (舍去),
(舍去),
综上所述,当2+![]() ≤m<
≤m<![]() 时,抛物线M2与直线AE有两个交点.
时,抛物线M2与直线AE有两个交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中央电视台的《朗读者》节目激发了同学们的读书热情,为了引导学生“多读书,读好书”,某校对八年级部分学生的课外阅读量进行了随机调查,整理调查结果发现,学生课外阅读的本数量少的有
 本,最多的有
本,最多的有 本,并根据调查结果绘制了不完整的图表,如下所示:
本,并根据调查结果绘制了不完整的图表,如下所示:本数(本)
频数(人数)
频率












合计



(
 )统计图表中的
)统计图表中的 __________,
__________, __________,
__________, __________.
__________.(
 )请将频数分布直方图补充完整.
)请将频数分布直方图补充完整.(
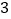 )求所有被调查学生课外阅读的平均本数.
)求所有被调查学生课外阅读的平均本数.(
 )若该校八年级共有
)若该校八年级共有 名学生,请你估计该校八年级学生课外阅读
名学生,请你估计该校八年级学生课外阅读 本及以上的人数.
本及以上的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】唐山世园会期间,游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收31万元.而该游乐场开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx.若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数.
(1)若维修保养费用第1个月为2万元,第2个月为4万元,求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大?并求出最大收益.
-
科目: 来源: 题型:
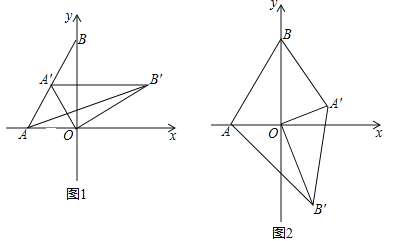
查看答案和解析>>【题目】如图1,在平面直角坐标系,O为坐标原点,点A(﹣1,0),点B(0,
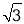 ).
).(1)求∠BAO的度数;
(2)如图1,将△AOB绕点O顺时针得△A′OB′,当A′恰好落在AB边上时,设△AB′O的面积为S1,△BA′O的面积为S2,S1与S2有何关系?为什么?
(3)若将△AOB绕点O顺时针旋转到如图2所示的位置,S1与S2的关系发生变化了吗?证明你的判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=2
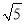 ,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.
,O是BC边的中点,点E是正方形内一动点,OE=2,连接DE,将线段DE绕点D逆时针旋转90°得DF,连接AE、CF.则线段OF长的最小值为_____.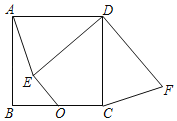
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校为调查学生的兴趣爱好,抽查了部分学生,并制作了如下表格与条形统计图:
频数
频率
体育
40
0.4
科技
25
a
艺术
b
0.15
其它
20
0.2
请根据上图完成下面题目:
(1)总人数为 人,a= ,b= .
(2)请你补全条形统计图.
(3)若全校有600人,请你估算一下全校喜欢艺术类学生的人数有多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣4,1),B(﹣2,3),C(﹣1,2).
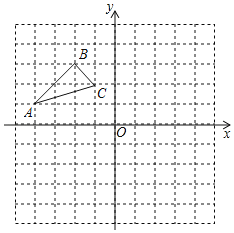
(1)画出△ABC关于原点O成中心对称的△A′B′C′,点A′,B′,C′分别是点A,B,C的对应点.
(2)求过点B′的反比例函数解析式.
(3)判断A′B′的中点P是否在(2)的函数图象上.
相关试题

