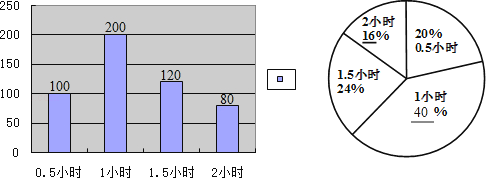
【题目】为了减轻学生的课业负担,某市教育行政部门规定中学生每天完成家庭作业的平均时间不能超过1.5小时,为了了解该市中学生课业负担情况,对部分学生每天完成家庭作业所用的时间进行了抽样调查,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)分别求出每天完成家庭作业所用的时间为“1小时”和“2小时”的学生人数占总人数的百分比,以及所用的时间为“1.5小时”的学生人数,并补全两个统计图;
(3)本次调查中,中学生每天完成家庭作业所用的平均时间是否符合要求?并说明理由.
参考答案:
【答案】
(1)
解:根据题意得:100÷20%=500(人),
则调查的学生数为500人;
(2)
解:每天完成家庭作业的时间为为1小时的人数为200人,占的百分比为 ![]() ×100%=40%;
×100%=40%;
每天完成家庭作业的时间为1.5小时的学生数为500×24%=120(人);
每天完成家庭作业的时间为2小时的学生数为500×16%=80(人),
补全统计图,如图所示:
(3)
解:符合要求,理由为:调查学生每天完成家庭作业的平均时间为0.5×20%+1×40%+1.5×24%+2×16%=0.1+0.4+0.36+0.32=1.18(小时)<1.5小时,则本次调查中,中学生每天完成家庭作业所用的平均时间符合要求.
【解析】(1)根据每天完成家庭作业的时间为0.5小时的人数除以所占的百分比即可确定出共调查的学生数;(2)由学生总数求出每天完成家庭作业的时间为1.5小时的学生数,补全条形统计图,求出每天完成家庭作业的时间为1小时的学生数占的百分比,补全扇形统计图即可;(3)求出调查学生每天完成家庭作业的平均时间,比较即可得到结果.
【考点精析】关于本题考查的扇形统计图和条形统计图,需要了解能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB = BC,D、E、F分别是BC、AC、AB边上的中点;
(1)求证:四边形BDEF是菱形;(2)若AB =12cm,求菱形BDEF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中的每个小正方形的边长都是1.A、B、C三点都在格点上.

(1)请你以格线所在直线为坐标轴建立平面直角坐标系,使A、B两点的坐标分别为A(﹣2,3),B(﹣3,1),并写出C点坐标;
(2)连接AB、BC、CA得△ABC,将△ABC向右平移4个单位,画出平移后的△A1B1C1;
(3)将△A1B1C1绕点B1按顺时针方向旋转90°,画出旋转后的△A2B1C2 , 并求出在旋转过程中线段A1B1所扫过的图形的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如下命题:①三角形的中线、角平分线、高都是线段;②三角形的三条高必交于一点;③三角形的三条角平分线必交于一点;④三角形的三条高必在三角形内.其中正确的是( )
A. ①② B. ①③ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。
(1)求证;OE=OF;(2)若BC=
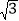 ,求AB的长。
,求AB的长。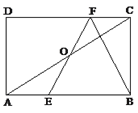
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程(组):
(1)
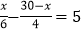 (2)
(2)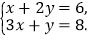
(3)
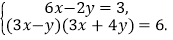
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=3,PB=1,PC= CD=2,CD⊥CP,求∠BPC的度数

相关试题

