【题目】如图1，在中，于E，，D是AE上的一点，且，连接BD，CD．

试判断BD与AC的位置关系和数量关系，并说明理由；

如图2，若将绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；

如图3，若将中的等腰直角三角形都换成等边三角形，其他条件不变．

试猜想BD与AC的数量关系，请直接写出结论；

你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．

参考答案：

【答案】(1)见解析;(2)见解析;(3) ①BD=AC理由见解析;见解析．

【解析】

（1）可以证明△BDE≌△ACE推出BD=AC，BD⊥AC．

（2）如图2中，不发生变化．只要证明△BED≌△AEC，推出BD=AC，∠BDE=∠ACE，由∠DEC=90°，推出∠ACE+∠EOC=90°，因为∠EOC=∠DOF，所以∠BDE+∠DOF=90°，可得∠DFO=180°－90°=90°，即可证明．

（3）①如图3中，结论：BD=AC，只要证明△BED≌△AEC即可．

②能；由△BED≌△AEC可知，∠BDE=∠ACE，推出∠DFC=180°－（∠BDE+∠EDC+∠DCF）=180°－（∠ACE+∠EDC+∠DCF）=180°－（60°+60°）=60°即可解决问题．

解：，，
理由是：延长BD交AC于F．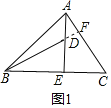

，
，
在和中
≌，
，，
，
，
，
，
，
；
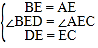
不发生变化．
如图2，令AC、DE交点为O

理由：，
，
，
在和中
≌，
，，
，
，
，
，
，
；

(3)；
证明：和是等边三角形，
，，，，
，
，
在和中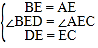
≌，
．

②夹角为．
解：如图3，令AC、BD交点为F，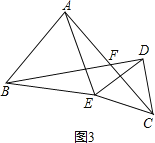

由①知≌，
，
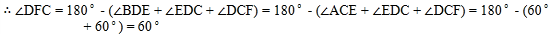，即BD与AC所成的角的度数为或

关闭