Question

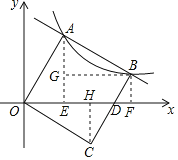
【题目】如图，平面直角坐标系中，O为坐标原点，正方形OABC的定点A，B都在反比例函数y=（k＞0，x＞0）的图象上，边BC与x轴交于点D，则 的值为（　　）

A. B. C. D.

Answer 1

【答案】D

【解析】

过A作AE⊥x轴于E，过B作BF⊥x轴于F，BG⊥AE于G，于是得到EF=BG，BF=GE，根据正方形的性质得到OA=AB，∠OAB=90°，根据余角的性质得到∠OAE=∠ABG，根据全等三角形的性质得到AG=OE，AE=BG，设A（a，），得到OE=AG=a，AE=BG=，求得B（+a，-a），得方程求得k=a2（负值舍去），过C作CH⊥x轴于H，根据相似三角形的性质即可得到结论．

解：过A作AE⊥x轴于E，过B作BF⊥x轴于F，BG⊥AE于G，

则EF=BG，BF=GE，

∵四边形OABC是正方形，

∴OA=AB，∠OAB=90°，

∴∠OAE+∠BAE=∠BAE+∠ABG=90°，

∴∠OAE=∠ABG，

在△AOE与△BAG中，，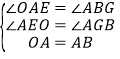

∴△AOE≌△BAG，

∴AG=OE，AE=BG，

设A（a，），

∴OE=AG=a，AE=BG=，

∴B（+a，-a），

∴（+a）（-a）=k，

解得k=a2（负值舍去），

∴B点的纵坐标为a，

BF=a，

过C作CH⊥x轴于H，

同理△AOE≌△OCH，

∴CH=OE=a，

∵CH⊥x轴，BF⊥x轴，

∴CH∥BF，

∴△BFD∽△CHD，

∴== =，

故选：D．