【题目】“低碳生活,绿色出行”,2017年1月,某公司向深圳市场新投放共享单车640辆.
(1)若1月份到4月份新投放单车数量的月平均增长率相同,3月份新投放共享单车1000辆.请问该公司4月份在深圳市新投放共享单车多少辆?
(2)考虑到自行车市场需求不断增加,某商城准备用不超过70000元的资金再购进A,B两种规格的自行车100辆,已知A型的进价为500元/辆,售价为700元/辆,B型车进价为1000元/辆,售价为1300元/辆。假设所进车辆全部售完,为了使利润最大,该商城应如何进货?
参考答案:
【答案】(1)新投放共享单1250辆;(2)为使利润最大,该商城应购进60辆A型车和40辆B型车
【解析】试题分析:(1)、首先设平均增长率为x,根据增长率问题的应用问题列出一元二次方程,求出x的值,从而得出4月份的销量;(2)、设购进A型车x辆,则购进B型车(100-x)辆,根据资金列出不等式,从而求出x的取值范围,然后根据题意列出利润与x的函数关系式,最后根据函数的增减性求出最值,得出进货方案.
试题解析:(1)、设平均增长率为![]() ,根据题意得:
,根据题意得: ![]()
解得: ![]() =0.25=25%或
=0.25=25%或![]() =-2.25 四月份的销量为:1000(1+25%)=1250辆,
=-2.25 四月份的销量为:1000(1+25%)=1250辆,
答:新投放共享单1250辆
(2)、设购进A型车![]() 辆,则购进B型车100-
辆,则购进B型车100- ![]() 辆,
辆,
根据题意得: ![]() 解得:
解得: ![]() .
.
利润w=(700-500)x+(1300-1000)(100-x)=200x+300(10-x)=-100x+30000
∵-100<0,∴W随着x的增大而减小.
当x=60时,利润最大![]() =2400
=2400
答:为使利润最大,该商城应购进60辆A型车和40辆B型车
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
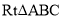 中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。
中,∠BAC=90°,∠C=30°,BC=2,⊙O是△ABC的外接圆,D是CB延长线上一点,且BD=1,连接DA,点P是射线DA上的动点。(1)求证DA是⊙O的切线;
(2)DP的长度为多少时,∠BPC的度数最大,最大度数是多少?请说明理由。
(3)点P运动的过程中,(PB+PC)的值能否达到最小,若能,求出这个最小值,若不能,说明理由.

-
科目: 来源: 题型:
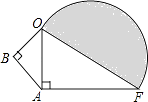
查看答案和解析>>【题目】如图所示,∠B=∠OAF=90°,BO=3cm,AB=4cm,AF=12cm,求图中半圆的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列多项式相乘的结果是a2﹣a﹣6的是( )
A.(a﹣2)(a+3)
B.(a+2)(a﹣3)
C.(a﹣6)(a+1)
D.(a+6)(a﹣1) -
科目: 来源: 题型:
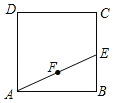
查看答案和解析>>【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|m﹣2|+(n﹣1)2=0,则m+2n的值为( )
A. ﹣1 B. 4 C. 0 D. ﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60°
相关试题

