【题目】如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,

(1)若∠ABC=30°,∠ACB=50°,求∠DAE的度数
(2)写出∠DAE与∠C-∠B的数量关系,并证明你的结论
参考答案:
【答案】(1)10°;(2)∠DAE=![]() (∠C-∠B),证明见解析.
(∠C-∠B),证明见解析.
【解析】
(1)利用三角形内角和定理求得∠BAC=100°,根据角平分线定义可知∠EAC=![]() ∠BAC,再利用三角形内角和先求出∠DAC,再求得∠DAE;
∠BAC,再利用三角形内角和先求出∠DAC,再求得∠DAE;
(2)按照(1)中思路,进行推导即可解决问题.
(1)解:∵∠B=30°,∠C=50°,
∴∠BAC=180°-∠B-∠C=100°,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC=50°
∠BAC=50°
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=180°-90°-50°=40°
∴∠DAE=∠EAC-∠DAC=50°-40°=10°
(2)解:∠BAC=180°-∠B-∠C,
∵AE平分∠BAC,
∴∠EAC=![]() ∠BAC=
∠BAC=![]() (180°-∠B-∠C)
(180°-∠B-∠C)
∵AD是高,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=180°-90°-∠C=90°-∠C,
∴∠DAE=∠EAC-∠DAC=![]() (180°-∠B-∠C)-(90°-∠C)
(180°-∠B-∠C)-(90°-∠C)
=![]() (∠C-∠B)
(∠C-∠B)
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有一项资助贫困生的公益活动由你来主持,每位参与者需交赞助费5元,活动规则如下:如图是两个可以自由转动的转盘,每个转盘被分成6个相等的扇形,参与者转动这两个转盘,转盘停止后,指针各自指向一个数字,(若指针在分格线上,则重转一次,直到指针指向某一数字为止),若指针最后所指的数字之和为12,则获得一等奖,奖金20元;数字之和为9,则获得二等奖,奖金10元;数字之和为7,则获得三等奖,奖金为5元;其余均不得奖;此次活动所集到的赞助费除支付获奖人员的奖金外,其余全部用于资助贫困生的学习和生活;
(1)分别求出此次活动中获得一等奖、二等奖、三等奖的概率;
(2)若此次活动有2000人参加,活动结束后至少有多少赞助费用于资助贫困生?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商家销售一款商品,进价每件80元,售价每件145元,每天销售40件,每销售一件需支付给商场管理费5元,未来一个月
 按30天计算
按30天计算 ,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天
,这款商品将开展“每天降价1元”的促销活动,即从第一天开始每天的单价均比前一天降低1元,通过市场调查发现,该商品单价每降1元,每天销售量增加2件,设第x天 且x为整数
且x为整数 的销售量为y件.
的销售量为y件. 直接写出y与x的函数关系式;
直接写出y与x的函数关系式; 设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元?
设第x天的利润为w元,试求出w与x之间的函数关系式,并求出哪一天的利润最大?最大利润是多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中.
中. 利用尺规作图,在BC边上求作一点P,使得点P到AB的距离
利用尺规作图,在BC边上求作一点P,使得点P到AB的距离 的长
的长 等于PC的长;
等于PC的长; 利用尺规作图,作出
利用尺规作图,作出 中的线段PD.
中的线段PD. 要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑
要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔描黑

-
科目: 来源: 题型:
查看答案和解析>>【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.学生借阅图书的次数统计表
借阅图书的次数
0次
1次
2次
3次
4次及以上
人数
7
13
a
10
3
请你根据统计图表中的信息,解答下列问题:
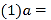 ______,
______,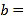 ______.
______.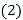 该调查统计数据的中位数是______,众数是______.
该调查统计数据的中位数是______,众数是______.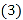 请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
请计算扇形统计图中“3次”所对应扇形的圆心角的度数; 若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数
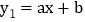 的图象与反比例函数
的图象与反比例函数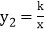 的图象交于点
的图象交于点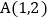 和
和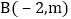 .
.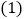 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式; 请直接写出
请直接写出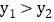 时,x的取值范围;
时,x的取值范围; 过点B作
过点B作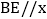 轴,
轴, 于点D,点C是直线BE上一点,若
于点D,点C是直线BE上一点,若 ,求点C的坐标.
,求点C的坐标.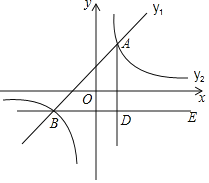
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 经过
经过 ,
, 两点,与y轴交于点C,连接AB,AC,BC.
两点,与y轴交于点C,连接AB,AC,BC.
 求抛物线的表达式;
求抛物线的表达式; 求证:AB平分
求证:AB平分 ;
; 抛物线的对称轴上是否存在点M,使得
抛物线的对称轴上是否存在点M,使得 是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
是以AB为直角边的直角三角形,若存在,求出点M的坐标;若不存在,请说明理由.
相关试题

