【题目】(请在括号里注明重要的推理依据)
如图,已知AM∥BN,∠A=60°.点P是射线AM上一动点(与点A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变化,请写出它们之间的关系,并说明理由;若变化,请写出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,∠ABC的度数是 .

参考答案:
【答案】(1)∠CBD=60°;(2)不变化,∠APB=2∠ADB,证明见解析;(3)∠ABC=30°.
【解析】
试题分析:(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN=60°+∠DBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,可求得∠ABC的度数.
试题解析: (1)∵AM∥BN,
∴∠A+∠ABN=180°,(两直线平行,同旁内角互补)
∵∠A=60°
∴∠ABN=120°
∵BC、BD分别平分∠ABP和∠PBN,
∴∠CBP=![]() ∠ABP, ∠DBP=
∠ABP, ∠DBP=![]() ∠NBP,
∠NBP,
∴∠CBD=![]() ∠ABN=60°
∠ABN=60°
(2)不变化,∠APB=2∠ADB
证明∴ ∵AM∥BN,
∴∠APB=∠PBN (两直线平行,内错角相等)
∠ADB=∠DBN (两直线平行,内错角相等)
又∵BD平分∠PBN,
∴∠PBN =2∠DBN
∴∠APB=2∠ADB
(3)∠ABC=30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线OB是一次函数y=2x的图象,点A的坐标是(0,2),点C在直线OB上且△ACO为等腰三角形,求C点坐标.
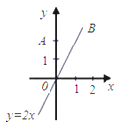
-
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)列式:x与20的差不小于0;
(2)若(1)中的x(单位:cm)是一个正方形的边长,现将正方形的边长增加2cm,则正方形的面积至少增加多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,6),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O—C—B—A—O的路线移动(即:沿着长方形移动一周).
(1)写出点B的坐标( ).
(2)当点P移动了4秒时,请在图中描出此时P点的位置,并求出点P的坐标.
(3)在移动过程中,当点P到x轴距离为5个单位长度时,求点P移动的时间.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直角三角形ABC的直角边AB=6,BC=8,将直角三角形ABC沿边BC的方向平移到三角形DEF的位置,DE交AC于点G,BE=2,三角形CEG的面积为13.5,下列结论:
①三角形ABC平移的距离是4; ②EG=4.5;
③AD∥CF; ④四边形ADFC的面积为6.
其中正确的结论是( )

A. ①② B. ②③ C. ③④ D. ②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级进行了模拟考试后,张老师对九(2)班全体同学“满分值为6分得一道解答题的得分”情况进行了统计,绘制成下表(学生得分均为整数分):

由于在填表时不慎把墨水滴在表格上,致使表中数据不完整,但已知全班同学此题的平均得分为4分,结合上表回答下列问题:
(1)九(2)班学生共有多少人?
(2)若本年级学生共有540人,请你用此样本估计整个年级有多少同学此题得满分?
相关试题

