【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用2种方法表示可得一个等式,求等式。
(2)若m+2n=7,mn=3,利用(1)的结论求m﹣2n的值.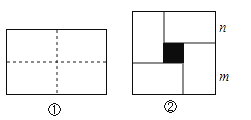
参考答案:
【答案】解:(1)(m+n)2﹣4mn=(m﹣n)2;故答案为:(m+n)2﹣4mn=(m﹣n)2
(2)(m﹣2n)2=(m+2n)2﹣8mn=25,
则m﹣2n=±5.
【解析】(1)大正方形的面积减去矩形的面积即可得出阴影部分的面积,也可得出三个代数式(m+n)2、(m﹣n)2、mn之间的等量关系;
(2)根据(1)所得出的关系式,可求出(m﹣2n)2 , 继而可得出m﹣2n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】多边形的外角和等于( )
A.180°
B.360°
C.720°
D.(n﹣2)180° -
科目: 来源: 题型:
查看答案和解析>>【题目】对分式
 ,
,  和
和  进行通分,它们的最简公分母为 .
进行通分,它们的最简公分母为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c+1,
①当b=1时,求这个二次函数的对称轴的方程;
②若c=
 b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?③若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足
 ,求二次函数的表达式.
,求二次函数的表达式.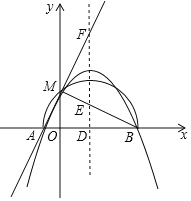
-
科目: 来源: 题型:
查看答案和解析>>【题目】 将抛物线y=x2-2x向上平移3个单位,再向右平移4个单位得到的抛物线解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】(黄石中考)一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表所示,现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销互动:购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为_______元.
型号
A
B
单个盒子容量(升)
2
3
单价(元)
5
6
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2
 ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500 米,桥的长度为1255米.
米,桥的长度为1255米.①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.

相关试题

