【题目】(黄石中考)一食堂需要购买盒子存放食物,盒子有A,B两种型号,单个盒子的容量和价格如表所示,现有15升食物需要存放且要求每个盒子要装满,由于A型号盒子正做促销互动:购买三个及三个以上可一次性返现金4元,则购买盒子所需要最少费用为_______元.
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
参考答案:
【答案】29
【解析】设购买A种型号盒子x个,购买盒子所需要费用为y元,则购买B种盒子的个数为![]() 个,①当0≤x<3时,y=5x+
个,①当0≤x<3时,y=5x+![]() ×6=x+30,∵k=1>0,∴y随x的增大而增大,
×6=x+30,∵k=1>0,∴y随x的增大而增大,
∴当x=0时,y有最小值,最小值为30元,②当3≤x时,y=5x+![]() ×6-4=26+x,∵k=1>0,∴y随x的增大而增大,∴当x=3时,y有最小值,最小值为29元,综合①②可得,购买盒子所需要最少费用为29元,故答案为:29.
×6-4=26+x,∵k=1>0,∴y随x的增大而增大,∴当x=3时,y有最小值,最小值为29元,综合①②可得,购买盒子所需要最少费用为29元,故答案为:29.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=﹣x2+bx+c+1,
①当b=1时,求这个二次函数的对称轴的方程;
②若c=
 b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?③若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足
 ,求二次函数的表达式.
,求二次函数的表达式.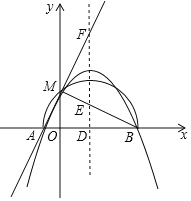
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)将图②中的阴影部分面积用2种方法表示可得一个等式,求等式。
(2)若m+2n=7,mn=3,利用(1)的结论求m﹣2n的值.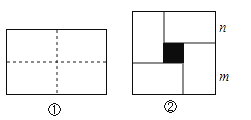
-
科目: 来源: 题型:
查看答案和解析>>【题目】 将抛物线y=x2-2x向上平移3个单位,再向右平移4个单位得到的抛物线解析式为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图示一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的
俯角为α其中tanα=2
 ,无人机的飞行高度AH为500
,无人机的飞行高度AH为500 米,桥的长度为1255米.
米,桥的长度为1255米.①求点H到桥左端点P的距离;
②若无人机前端点B测得正前方的桥的右端点Q的俯角为30°,求这架无人机的长度AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把一些书分给几名同学,若每人分11本,则有剩余,若( ),依题意,设有x名同学,可列不等式7(x+4)>11x.
A.每人分7本,则剩余4本
B.每人分7本,则剩余的书可多分给4个人
C.每人分4本,则剩余7本
D.其中一个人分7本,则其他同学每人可分4本
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
 与抛物线
与抛物线 相交于A、B两点,与
相交于A、B两点,与 轴交于点M,M、N关于
轴交于点M,M、N关于 轴对称,连接AN、BN.
轴对称,连接AN、BN.
(1)①求A、B的坐标;
②求证:∠ANM=∠BNM;
(2)如图,将题中直线
 变为
变为 ,抛物线
,抛物线 变为
变为 ,其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
,其他条件不变,那么∠ANM=∠BNM是否仍然成立?请说明理由.
相关试题

