【题目】如图,抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 在抛物线上,点
在抛物线上,点![]() 在抛物线的对称轴上,是否存在以点
在抛物线的对称轴上,是否存在以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在。求出所有符合条件的点
为顶点的四边形是平行四边形?若存在。求出所有符合条件的点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

参考答案:
【答案】(1) 抛物线解析式为![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据当![]() 时,
时,![]() 可知C(0,-3)根据
可知C(0,-3)根据![]() ,可知B(-1,0)利用待定系数法求出抛物线的解析式即可.(2)如图:连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(-1,-3),可知∠BAC=45°,设D(0,m),则OD=|m|根据∠BDO=∠BAC=45°,即可得到结论;(3)设M(a,a2-2a-3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图:过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(-2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.
,可知B(-1,0)利用待定系数法求出抛物线的解析式即可.(2)如图:连接AC,作BF⊥AC交AC的延长线于F,根据已知条件得到AF∥x轴,得到F(-1,-3),可知∠BAC=45°,设D(0,m),则OD=|m|根据∠BDO=∠BAC=45°,即可得到结论;(3)设M(a,a2-2a-3),N(1,n),①以AB为边,则AB∥MN,AB=MN,如图:过M作ME⊥对称轴y于E,AF⊥x轴于F,于是得到△ABF≌△NME,证得NE=AF=3,ME=BF=3,得到M(4,5)或(-2,11);②以AB为对角线,BN=AM,BN∥AM,如图3,则N在x轴上,M与C重合,于是得到结论.
(1)当![]() 时,
时,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.![]() ,
,![]() ,
,
![]() 抛物线解析式为
抛物线解析式为![]() .
.
(2)连接AC,作BF⊥AC交AC的延长线于F,
∵A(2,-3),C(0,-3),
∴AF∥x轴,
∴F(-1,-3),
∴BF=3,AF=3,
∴∠BAC=45°,
设D(0,m),则OD=|m|,
∵∠BDO=∠BAC,
∴∠BDO=45°,
∴OD=OB=1,
∴|m|=1,
∴m=±1,
∴D1(0,1),D2(0,-1);
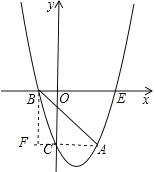
(3)设M(a,a2-2a-3),N(1,n),
①以AB/span>为边,则AB∥MN,AB=MN,过M作ME⊥对称轴y于E,AF⊥x轴于F,
则△ABF≌△NME,
∴NE=AF=3,ME=BF=3,
∴|a-1|=3,
∴a=4或a=-2,
∴M(4,5)或(-2,5);
②以AB为对角线,BN=AM,BN∥AM,如图,
则N在x轴上,M与C重合,
∴M(0,-3),
综上所述,存在以点A,B,M,N为顶点的四边形是平行四边形,M(4,5)或(-2,5)或(0,-3).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 边为直径的⊙
边为直径的⊙ 经过点
经过点 ,
, 是⊙
是⊙ 上一点,连结
上一点,连结 交
交 于点
于点 ,且
,且 ,
, .
.(1)试判断
 与⊙
与⊙ 的位置关系,并说明理由;
的位置关系,并说明理由; (2)若点
 是弧
是弧 的中点,已知
的中点,已知 ,求
,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知;如图1,菱形ABCD的边AB在x轴上,点B的坐标为
 ,点C在y轴上,
,点C在y轴上,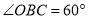 .
.
(1)求点A的坐标;
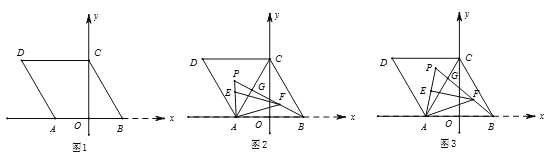
(2)如图2,连接AC,点P为△ACD内一点,BP与AC交于点G,
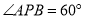 ,点E、F分别在线段AP、BP上,且
,点E、F分别在线段AP、BP上,且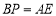 .若
.若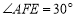 ,求
,求 的值;
的值;(3)如图3,在(2)的条件下,当
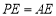 时,试判断△PAF形状并说明理由.
时,试判断△PAF形状并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左边到右边的变形,是因式分解的是( )
A.y
 ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3C.x(x﹣1)=x
 ﹣xD.m
﹣xD.m +n
+n =(m+n)(m﹣n)
=(m+n)(m﹣n) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出△ABC 关于 y 轴对称的△A1B1C1并写出坐标;
(2)求出△A1B1C1的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点B、F、C、E在同一直线上,AC、DF相交于点G,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AC=DF,BF=EC.求证:

(1)△ABC≌△DEF;
(2)FG=CG.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
相关试题

