【题目】已知;如图1,菱形ABCD的边AB在x轴上,点B的坐标为![]() ,点C在y轴上,
,点C在y轴上,![]() .
.
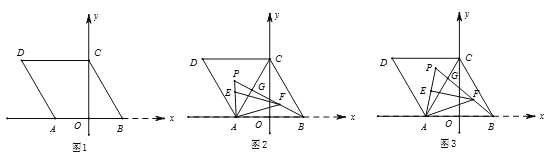
(1)求点A的坐标;
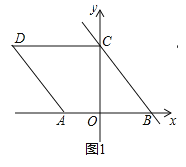
(2)如图2,连接AC,点P为△ACD内一点,BP与AC交于点G,![]() ,点E、F分别在线段AP、BP上,且
,点E、F分别在线段AP、BP上,且![]() .若
.若![]() ,求
,求![]() 的值;
的值;
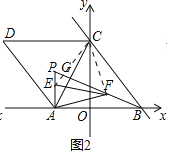
(3)如图3,在(2)的条件下,当![]() 时,试判断△PAF形状并说明理由.
时,试判断△PAF形状并说明理由.
参考答案:
【答案】(1)A(﹣![]() ,0).(2)49.(3)见解析
,0).(2)49.(3)见解析
【解析】
(1)利用勾股定理求出BC,再根据菱形的性质进行计算即可解决问题;
(2)如图2中,连接CE、CF.先证明△ABC是等边三角形,得到∠ACB=60°,再求得△CEF是等边三角形,根据等边三角形的性质得到∠AFC =90°,再由勾股定理得到AF2+CF2=AC2=49;
(3)如图3中,延长CE交FA的延长线于H,作PQ⊥AB于Q,PK⊥OC于K,在BP设截取BT=PA,连接AT、CT、CF、PC,根据等边三角形的性质,结合题意得到△CPE≌△HAE,再结合题意由全等三角形的性质得到△ACP≌△BCT,根据全等三角形的性质得到△CPT是等边三角形,再根据题意即可证明△APF是等边三角形.
(1)如图1中,
∵y=-﹣![]() x+
x+![]() ,
,
∴B(![]() ,0),C(0,
,0),C(0,![]() ),
),
∴BO=![]() ,OC=
,OC=![]() ,
,
在Rt△OBC中,BC=![]() =7,
=7,
∵四边形ABCD是菱形,
∴AB=BC=7,
∴OA=AB-OB=7-![]() =
=![]() ,
,
∴A(-![]() ,0).
,0).
(2)如图2中,连接CE、CF.
∵OA=OB,CO⊥AB,
∴AC=BC=7,
∴AB=BC=AC,
∴△ABC是等边三角形,
∴∠ACB=60°,
∵∠APB=60°,
∴∠APB=∠ACB,
∵∠PAG+∠APB=∠AGB=∠CBG+∠ACB,
∴∠PAG=∠CBG,∵AE=BF,
∴△ACE≌△BCF,
∴CE=CF,∠ACE=∠BCF,
∴∠ECF=∠ACF+∠ACE=∠ACF+∠BCF=∠ACB=60°,
∴△CEF是等边三角形,
∴∠CFE=60°,EF=FC,
∵∠AFE=30°,
∴∠AFC=∠AFE+∠CFE=90°,
在Rt△ACF中,AF2+CF2=AC2=49,
∴AF2+EF2=49.
(3)如图3中,延长CE交FA的延长线于H,作PQ⊥AB于Q,PK⊥OC于K,在BP设截取BT=PA,连接AT、CT、CF、PC.
∵△CEF是等边三角形,
∴∠CEF=60°,EC=CF,
∵∠AFE=30°,∠CEF=∠H+∠EFH,
∴∠H=∠CEF-∠EFH=30°,
∴∠H=∠EFH,
∴EH=EF,
∴EC=EH,
∵PE=AE,∠PEC=∠AEH,
∴△CPE≌△HAE,
∴∠PCE=∠H,
∴PC∥FH,
∵∠CAP=∠CBT,AC=BC,
∴△ACP≌△BCT,
∴CP=CT,∠ACP=∠BCT,
∴∠PCT=∠ACB=60°,
∴△CPT是等边三角形,
∴CT=PT,∠CPT=∠CTP=60°,
∵CP∥FH,
∴∠HFP=∠CPT=60°,
∵∠APB=60°,
∴△APF是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴
 .(依据1)
.(依据1)∵BE=AB,∴
 .∴EM=DM.
.∴EM=DM.即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣4,2)、B(n,﹣4)两点是一次函数y=kx+b和反比例函数y=
 图象的两个交点.
图象的两个交点.(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)观察图象,直接写出不等式kx+b﹣
 >0的解集.
>0的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
 边为直径的⊙
边为直径的⊙ 经过点
经过点 ,
, 是⊙
是⊙ 上一点,连结
上一点,连结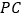 交
交 于点
于点 ,且
,且 ,
, .
.(1)试判断
 与⊙
与⊙ 的位置关系,并说明理由;
的位置关系,并说明理由; (2)若点
 是弧
是弧 的中点,已知
的中点,已知 ,求
,求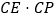 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列从左边到右边的变形,是因式分解的是( )
A.y
 ﹣5y﹣6=(y﹣6)(y+1)B.a
﹣5y﹣6=(y﹣6)(y+1)B.a +4a﹣3=a(a+4)﹣3
+4a﹣3=a(a+4)﹣3C.x(x﹣1)=x
 ﹣xD.m
﹣xD.m +n
+n =(m+n)(m﹣n)
=(m+n)(m﹣n) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 经过点
经过点 ,与
,与 轴负半轴交于点
轴负半轴交于点 ,与
,与 轴交于点
轴交于点 ,且
,且 .
.(1)求抛物线的解析式;
(2)点
 在
在 轴上,且
轴上,且 ,求点
,求点 的坐标;
的坐标;(3)点
 在抛物线上,点
在抛物线上,点 在抛物线的对称轴上,是否存在以点
在抛物线的对称轴上,是否存在以点 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在。求出所有符合条件的点
为顶点的四边形是平行四边形?若存在。求出所有符合条件的点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出△ABC 关于 y 轴对称的△A1B1C1并写出坐标;
(2)求出△A1B1C1的面积.
相关试题

