Question

【题目】如图，正方形ABCD的面积为16cm2，△AEF为等腰直角三角形，∠E=90°，AE和BC交于点G，AF和CD交于点H，则△CGH的周长（　　）

A. 4cmB. 6cmC. 8cmD. 10cm

Answer 1

【答案】C

【解析】

延长CB至M，使BM=DH，连接AM；易证△ABM≌△ADH与△AMG≌△AHG，得到△CGH的周长=GH+CG+CH=GM+CG+CH=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=8．

延长CB至M，使BM=DH，连接AM；如图所示：

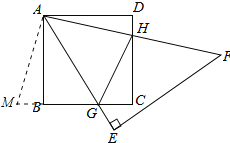
∵四边形ABCD是正方形，正方形ABCD的面积为16cm2，

∴AB=BC=CD=4cm，∠BAD=∠ABC=∠D=90°，

∴∠ABM=90°，

在△ABM和△ADH中，AB=AD,∠ABM=∠D=90°，BM=DH，

∴△ABM≌△ADH（SAS），

∴AM=AH，∠BAM=∠DAH，

∵△AEF是等腰直角三角形，

∴∠HAG=45°，

∴∠BAG+∠DAH=45°，

∴∠MAG=45°，

在△AMG和△AHG中，AM=AH,∠MAG=∠HAG,AG=AG

∴△AMG≌△AHG（SAS），

∴GM=GH，

∴△CGH的周长=GH+CG+CH=GM+CG+CH

=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=8．

故选：C．