【题目】如图1,平面内,![]() ,
,![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)当![]() 时,取
时,取![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,如图2,判断
,如图2,判断![]() 的形状,并加以证明.
的形状,并加以证明.
参考答案:
【答案】(1)证明见解析;(2)△AMN为等腰直角三角形,证明见解析.
【解析】
(1)由![]() 可得
可得![]() ,根据
,根据![]() ,
,![]() ,
,![]() ,利用SAS即可判定△ACD≌△ABE即可解决问题;
,利用SAS即可判定△ACD≌△ABE即可解决问题;
(2)先根据SAS判定△ABM≌△ACN,再根据全等三角形的性质,得出AM=AM,∠CAN=∠BAM,最后根据∠BAC=90°即可得到∠MAN=90°,进而得到△AMN为等腰直角三角形.
(1)如图1,∵![]() ,
,
∴![]() ,
,
在△DAC和△BAE中,
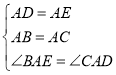 ,
,
∴△DAC≌△BAE(SAS),
∴![]() ;
;
(2)△AMN为等腰直角三角形.
证明:由(1)可得,BE=CD,
∵CD,BE的中点分别为点N、M,
∴BM=CN,
∵△DAC≌△BAE,
∴∠ABM=∠ACN,
在△ABM和△ACN中,
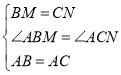 ,
,
∴△ABM≌△ACN(SAS),
∴AM=AN,且∠BAM=∠CAN,
又∵∠CAN+∠NAB=90°,
∴∠MAB+∠BAN=90°,
∴∠MAN=90°,
∴△AMN为等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系;
②去超市购买同一单价的水果,所付费用与水果数量的关系;
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系;
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AB、AC于点M、N,再分别以点M、N为圆心,大于
 MN的长为半径画弧,两弧交于点P,射线AP交边BC于点D.下列说法错误的是( )
MN的长为半径画弧,两弧交于点P,射线AP交边BC于点D.下列说法错误的是( )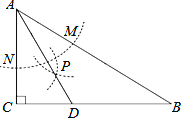
A.
 B. 若
B. 若 ,则点D到AB的距离为2
,则点D到AB的距离为2C. 若
 ,则
,则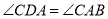 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道整数
 除以整数
除以整数 (其中
(其中 ),可以用竖式计算,例如计算
),可以用竖式计算,例如计算 可以用整式除法如图:
可以用整式除法如图: ,所以
,所以 .
.类比此方法,多项式除以多项式一般也可以用竖式计算,步骤如下:
①把被除式,除式按某个字母作降幂排列,并把所缺的项用零补齐;
②用被除式的第一项除以除式第一项,得到商式的第一项;
③用商式的第一项去乘除式,把积写在被除式下面(同类对齐),消去相等项;
④把减得的差当作新的被除式,再按照上面的方法继续演算,直到余式为零或余式的次数低于除式的次数时为止,被除式=除式×商式+余式,若余式为零,说明这个多项式能被另一个多项式整除.
例如:计算
 .
.可用整式除法如图:

所以
 除以
除以
商式为
 ,余式为0
,余式为0根据阅读材料,请回答下列问题:
(1)
 .
.(2)
 ,商式为 ,余式为 .
,商式为 ,余式为 .(3)若关于
 的多项式
的多项式 能被三项式
能被三项式 整除,且
整除,且 均为整数,求满足以上条件的
均为整数,求满足以上条件的 的值及商式.
的值及商式. -
科目: 来源: 题型:
查看答案和解析>>【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次
第二次
第三次
第四次
第五次
第六次
甲
10
8
9
8
10
9
乙
10
7
10
10
9
8
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
计算方差的公式:s2=
 [(x1-
[(x1- )2+(x2-
)2+(x2- )2++(xn-
)2++(xn- )2]
)2] -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的面积为16cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长( )

A. 4cmB. 6cmC. 8cmD. 10cm
相关试题

