【题目】阅读下面材料:
如图1,已知线段AB、CD相交于点O,且AB=CD,请你利用所学知识把线段AB、CD转移到同一三角形中。
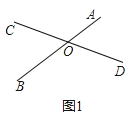
小强同学利用平移知识解决了此问题,具体做法如下:
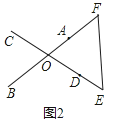
如图2,延长OD至点E,使DE=CO,延长OA至点F,使AF=OB,连接EF,则△OEF为所求的三角形。
请你仔细体会小强的做法,探究并解答下列问题:
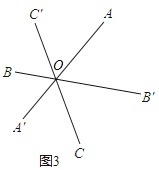
如图3,长为2的三条线段AA′,BB′,CC′交于一点O,并且∠B′OA=∠C′OB=∠A′OC=60°;
(1)请你把三条线段AA′,BB′,CC′ 转移到同一三角形中。(简要叙述画法)
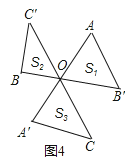
(2)连接AB′、BC′、CA′,如图4,设△AB′O、△BC′O、△CA′O的面积分别为S1、S2、S3,则S1+S2+S3________(填“>”或“<”或“=”)。
参考答案:
【答案】![]()
【解析】试题分析:(1)根据材料得出延长OA至点E,使AE=A′O;延长OB′至点F,使B′F=OB;连接EF,则△OEF为所求;
(2)根据平移的性质首先得出![]() ,再利用图象得出S1+S2+S3<S△EOF.
,再利用图象得出S1+S2+S3<S△EOF.
试题解析:
(1)如图所示:画法:①延长OA至点E,使AE=A′O;②延长OB′至点F,使B′F=OB;③连接EF,则△OEF为所求的三角形。
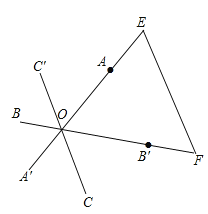
(2)∵长为2的三条线段AA′,BB′,CC′交于一点O,
并且∠B′OA=∠C′OB=∠A′OC=60°;
∴△OEF为边长为2的等边三角形,∴![]() ,
,
在EF上截取EQ=CO,则QF=C′O,
∴可得△A′CO≌△QEA,△B′FQ≌△OBC′,
如图所示:
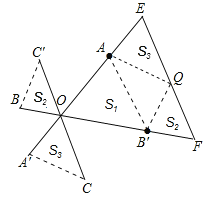
则![]() 。
。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=
 (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2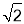 ,点A的纵坐标为4.
,点A的纵坐标为4.(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上的A、B两点分别对应数字a、b,且a、b满足|4a-b|+(a-4)2=0

(1)a= ,b= ,并在数轴上面出A、B两点;
(2)若点P从点A出发,以每秒3个单位长度向x轴正半轴运动,求运动时间为多少时,点P到点A的距离是点P到点B距离的2倍;
(3)数轴上还有一点C的坐标为30,若点P和点Q同时从点A和点B出发,分别以每秒3个单位长度和每秒1个单位长度的速度向C点运动,P点到达C点后,再立刻以同样的速度返回,运动到终点A.求点P和点Q运动多少秒时,P、Q两点之间的距离为4,并求此时点Q对应的数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市正在举行文化艺术节活动,一商店抓住商机,决定购进甲,乙两种艺术节纪念品.若购进甲种纪念品4件,乙种纪念品3件,需要550元,若购进甲种纪念品5件,乙种纪念品6件,需要800元.
(1)求购进甲、乙两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共80件,其中甲种纪念品的数量不少于60件.考虑到资金周转,用于购买这80件纪念品的资金不能超过7100元,那么该商店共有几种进货方案7
(3)若销售每件甲种纪含晶可获利润20元,每件乙种纪念品可获利润30元.在(2)中的各种进货方案中,若全部销售完,哪一种方案获利最大?最大利利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3
 时,求线段DH的长.
时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )

A.
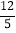 B. 4 C.
B. 4 C. 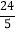 D. 5
D. 5 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△
 沿
沿 翻折得到△
翻折得到△ ,连接
,连接 ,取
,取 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
相关试题

