【题目】已知点P是矩形ABCD边AB上的任意一点(与点A、B不重合)
(1)如图①,现将△PBC沿PC翻折得到△PEC;再在AD上取一点F,将△PAF沿PF翻折得到△PGF,并使得射线PE、PG重合,试问FG与CE的位置关系如何,请说明理由;
(2)在(1)中,如图②,连接FC,取FC的中点H,连接GH、EH,请你探索线段GH和线段EH的大小关系,并说明你的理由;
(3)如图③,分别在AD、BC上取点F、C’,使得∠APF=∠BPC’,与(1)中的操作相类似,即将△PAF沿PF翻折得到△PFG,并将△![]() 沿
沿![]() 翻折得到△
翻折得到△![]() ,连接
,连接![]() ,取
,取![]() 的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.
的中点H,连接GH、EH,试问(2)中的结论还成立吗?请说明理由.

参考答案:
【答案】(1)FG∥CE,在矩形ABCD中,∠A=∠B=90°,由题意得,∠G=∠A=90°,∠PEC=∠B=90°,∴∠GEC=90°,∴∠G=∠GEC,∴FG∥CE。
(2)GH=EH。延长GH交CE于点M,由(1)得,FG∥CE,∴∠GFH=∠MCH,∵H为CF的中点,∴FH=CH,又∵∠GHF=∠MHC,∴△GFH≌△MHC,∴GH=HM=![]() ,∵∠GEC=90°,∴EH=
,∵∠GEC=90°,∴EH=![]() ,∴GH=EH。
,∴GH=EH。
(3)(2)中的结论还成立。取PF的中点M,![]() 的中点N,∵∠FGP=90°,M为PF的中点,∴
的中点N,∵∠FGP=90°,M为PF的中点,∴![]() ,
,![]() ,
,![]() ∥
∥![]() ,∴GM=PM,∴∠GPF=∠MGP,∴∠GMF=∠GPF+∠MGP=2∠GPF,∵H为
,∴GM=PM,∴∠GPF=∠MGP,∴∠GMF=∠GPF+∠MGP=2∠GPF,∵H为![]() 的中点,M为PF的中点,∴
的中点,M为PF的中点,∴![]() ,同理
,同理![]() ,
,![]() ,HN∥PF,∠
,HN∥PF,∠![]() ,∴GM=HN,HM=EN。∵∠GPF=∠FPA,
,∴GM=HN,HM=EN。∵∠GPF=∠FPA,![]() ,又
,又![]() ,∴∠GPF=
,∴∠GPF=![]() ,∴∠GMF=∠
,∴∠GMF=∠![]() ,∵
,∵![]() ∥
∥![]() ,HN∥PF,∴四边形HMPN为平行四边形,∴∠HMF=∠
,HN∥PF,∴四边形HMPN为平行四边形,∴∠HMF=∠![]() ,∴∠GMH=∠HNE,∵GM=HN,HM=EN,∴△GMH≌△HNE,∴GH=HE。
,∴∠GMH=∠HNE,∵GM=HN,HM=EN,∴△GMH≌△HNE,∴GH=HE。
【解析】(1)根据矩形的性质以及轴对称的性质可以得到∠G=∠GEC=90°,根据内错角相等,即可证明两
条直线平行;
延长GH交CE于点M,结合(1)中的结论证明△GFH≌△MHC,再运用直角三角形斜边上的中线等于
斜边的一半进行证明结论;
取PF的中点M,PC'的中点N,根据直角三角形的斜边上的中线等于斜边的一半以及三角形的中位线
定理得到平行四边形,这几个平行四边形的性质证明要证明的两条线段所在的两个三角形全等,从而证明结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料:
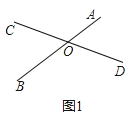
如图1,已知线段AB、CD相交于点O,且AB=CD,请你利用所学知识把线段AB、CD转移到同一三角形中。
小强同学利用平移知识解决了此问题,具体做法如下:
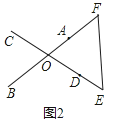
如图2,延长OD至点E,使DE=CO,延长OA至点F,使AF=OB,连接EF,则△OEF为所求的三角形。
请你仔细体会小强的做法,探究并解答下列问题:
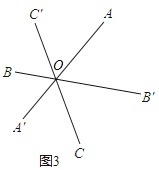
如图3,长为2的三条线段AA′,BB′,CC′交于一点O,并且∠B′OA=∠C′OB=∠A′OC=60°;
(1)请你把三条线段AA′,BB′,CC′ 转移到同一三角形中。(简要叙述画法)
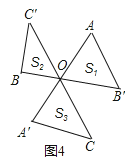
(2)连接AB′、BC′、CA′,如图4,设△AB′O、△BC′O、△CA′O的面积分别为S1、S2、S3,则S1+S2+S3________(填“>”或“<”或“=”)。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3
 时,求线段DH的长.
时,求线段DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )

A.
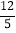 B. 4 C.
B. 4 C. 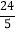 D. 5
D. 5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A,B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120nmile,乙巡逻艇每小时航行50nmile,航向为北偏西40°,求甲巡逻艇的航向.
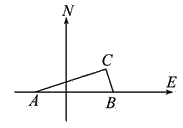
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形
②以
 ,
,  ,
,  的长为边的三条线段能组成一个三角形
的长为边的三条线段能组成一个三角形③以a+b,c+h,h的长为边的三条线段能组成直角三角形
④以
 ,
,  ,
,  的长为边的三条线段能组成直角三角形
的长为边的三条线段能组成直角三角形其中所有正确结论的序号为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某区教研部门对本区初二年级的学生进行了一次随机抽样问卷调查,其中有这样一个问题:老师在课堂上放手让学生提问和表达( )
A.从不 B.很少 C.有时 D.常常 E.总是
答题的学生在这五个选项中只能选择一项.下面是根据学生对该问题的答卷情况绘制的两幅不完整的统计图.
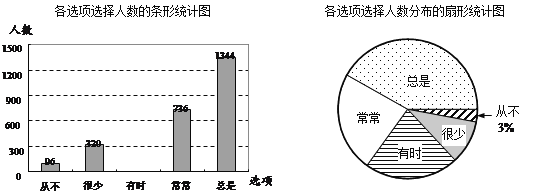
根据以上信息,解答下列问题:
(1)该区共有 名初二年级的学生参加了本次问卷调查;
(2)请把这幅条形统计图补充完整;
(3)在扇形统计图中,“总是”的圆心角为 .(精确到度)
相关试题

