【题目】如图,在平面直角坐标系中,一次函数y=mx+n(m≠0)的图象与反比例函数y=![]() (k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2
(k≠0)的图象交于第一、三象限内的A、B两点,与y轴交于点C,过点B作BM⊥x轴,垂足为M,BM=OM,OB=2![]() ,点A的纵坐标为4.
,点A的纵坐标为4.
(1)求该反比例函数和一次函数的解析式;
(2)连接MC,求四边形MBOC的面积.

参考答案:
【答案】(1)反比例函数的解析式为y=![]() ,一次函数的解析式为y=2x+2;(2)4.
,一次函数的解析式为y=2x+2;(2)4.
【解析】
试题分析:(1)根据题意可得B的坐标,从而可求得反比例函数的解析式,进行求得点A的坐标,从而可求得一次函数的解析式;
(2)根据(1)中的函数关系式可以求得点C,点M,点B,点O的坐标,从而可求得四边形MBOC的面积.
试题解析:(1)由题意可得,
BM=OM,OB=2![]() ,
,
∴BM=OM=2,
∴点B的坐标为(﹣2,﹣2),
设反比例函数的解析式为y=![]() ,
,
则﹣2=![]() ,得k=4,
,得k=4,
∴反比例函数的解析式为y=![]() ,
,
∵点A的纵坐标是4,
∴4=![]() ,得x=1,
,得x=1,
∴点A的坐标为(1,4),
∵一次函数y=mx+n(m≠0)的图象过点A(1,4)、点B(﹣2,﹣2),
∴![]() ,得
,得![]() ,
,
即一次函数的解析式为y=2x+2;
(2)∵y=2x+2与y轴交与点C,
∴点C的坐标为(0,2),
∵点B(﹣2,﹣2),点M(﹣2,0),点O(0,0),
∴OM=2,OC=2,MB=2,
∴四边形MBOC的面积是:![]() =4.
=4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知ax=5,ax+y=30,求ax+ay的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k=
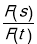 ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】五一节期间,电器市场火爆,某商店需要购进一批电视机和洗衣机,根据市场调查,电视机与洗衣机的进价和售价如下表:
类别
电视机
洗衣机
进价(元/台)
1800
1500
售价(元/台)
2000
1600
若该商店计划电视机和洗衣机共100台,设购进电视机x台,获得的总利润y元.
(1)求出y与x的函数关系;
(2)已知商店最多筹集资金161800元,求购进多少台电视机,才能使商店销售购进的电视机与洗衣机完毕后获得的利润最多?并求出最多利润.(利润=售价﹣进价) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
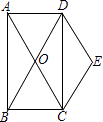
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】在菱形ABCD中,∠B=60°,AB=4,动点M以每秒1个单位的速度从点A出发运动到点B,点N以相同的速度从点B出发运动到点C,两点同时出发,过点M作MP⊥AB交直线CD于点P,连接NM、NP,设运动时间为t秒.
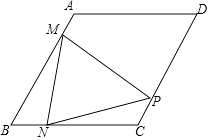
(1)当t=2时,∠NMP=度;
(2)求t为何值时,以A、M、C、P为顶点的四边形是平行四边形;
(3)当△NPC为直角三角形时,求此时t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2)4+3×(﹣1)5﹣(﹣2).
相关试题

