【题目】阅读下面的推理过程,在括号内填上推理的依据,如图:

∵∠1+∠2=180°,∠2+∠4=180°(已知)
∴∠1=∠4( )
∴c∥a( )
又∵∠2+∠3=180°(已知 )
∠3=∠6( )
∴∠2+∠6=180°( )
∴a∥b( )
∴c∥b( )
参考答案:
【答案】见解析
【解析】
依据同角的补角相等可证明∠1=∠4,依据平行线的判定定理可证明a∥c,依据对顶角的性质和等量代换可证明∠2+∠6=180°,最后依据平行线的判定定理和平行公理的推论进行证明即可.
因为∠1+∠2=180°,∠2+∠4=180°(已知),
所以∠1=∠4,(同角的补角相等)
所以a∥c.(内错角相等,两直线平行)
又因为∠2+∠3=180°(已知)
∠3=∠6(对顶角相等)
所以∠2+∠6=180°,(等量代换)
所以a∥b.(同旁内角互补,两直线平行)
所以c∥b.(平行与同一条直线的两条直线平行).
故答案为:同角的补角相等;内错角相等,两直线平行;对顶角相等;等量代换;同旁内角互补,两直线平行;平行与同一条直线的两条直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P、Q分别是⊙O的内接正五边形的边AB、BC上的点,BP=CQ,则∠POQ= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列一段文字:在直角坐标系中,已知两点的坐标是M(x1,y1),N(x2,y2)),M,N两点之间的距离可以用公式MN=
 计算.解答下列问题:
计算.解答下列问题:
(1)若点P(2,4),Q(﹣3,﹣8),求P,Q两点间的距离;
(2)若点A(1,2),B(4,﹣2),点O是坐标原点,判断△AOB是什么三角形,并说明理由.
(3)已知点A(5,5),B(-4,7),点P在x轴上,且要使PA+PB的和最小,求PA+PB的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AC、BD交于点O,点P、E分别是直线BD、BC上的动点,且PE=PC,过点E作EF∥AC交直线BD于点F.


(1)如图1,当∠COD=90°时,判断△BEF的形状,并说明理由;
(2)如图2,当点P在线段BO上时,求证:OP=BF;
(3)当∠COD=60°,CD=3时,请直接写出当△PEF成为直角三角形时的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的是小华从家里跑步去体育馆,在那里锻炼了一阵后又走到文具店去买笔,然后走回家,其中x表示时间,y表示小华离家的距离.根据图像回答下列问题:
(1)小华在体育馆锻炼了_____分钟;
(2)体育馆离文具店______千米;
(3)小华从家跑步到体育馆,从文具店散步回家的速度分别是多少千米/分钟?

-
科目: 来源: 题型:
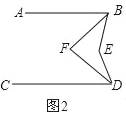
查看答案和解析>>【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,有若干个整数点(横、纵坐标均为整数),其顺序按图中方向排列,如(1,0),(2,0),(2,1),(3,1),(3,0)…… 根据这个规律探索可得,第50个点的坐标为( )
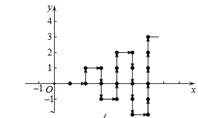
A. (10,-5)B. (10,-1) C. (10,0) D. (10,1)
相关试题

