Question

【题目】在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；

（2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD﹣BE；

（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．

Answer 1

【答案】（1）①证明见解析；②证明见解析；（2）证明见解析；（3）DE=BE﹣AD．

【解析】

（1）根据同角的余角相等得到∠ACD=∠CBE，即可证明△ADC≌△CEB；

（2）根据全等三角形的性质得到AD=CE，DC=EB，即可证明DE=AD﹣BE；

（3）与（1）的证明方法类似，证的△ADC≌△CEB，得出AD=CE，DC=EB，即可得出DE、AD、BE的等量关键.

（1）∵∠ACB=90°

∴∠ACD+∠BCE=90°

又∵AD⊥MN，BE⊥MN

∴∠ADC=∠CEB=90°

∴∠BCE+∠CBE=90°

∴∠ACD=∠CBE

在△ADC和△CEB中，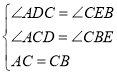

∴△ADC≌△CEB

∴AD=CE，DC=BE

∴DE=DC+CE=BE+AD；

（2）在△ADC和△CEB中，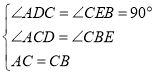

∴△ADC≌△CEB

∴AD=CE，DC=EB

∴DE=CE﹣DC=AD﹣EB；

（3）DE=BE﹣AD．

在△ADC和△CEB中，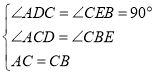

∴△ADC≌△CEB

∴AD=CE，DC=BE

∴DE=DC﹣CE=BE﹣AD．