【题目】小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行使路程y(千米)与行驶时间x(分钟)之间的函数图象如图所示. 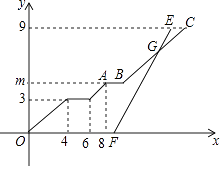
(1)求点A的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车?并求此时他们距学校站点的路程.
参考答案:
【答案】
(1)解:校车的速度为3÷4=0.75(千米/分钟),
点A的纵坐标m的值为3+0.75×(8﹣6)=4.5.
答:点A的纵坐标m的值为4.5
(2)解:校车到达学校站点所需时间为9÷0.75+4=16(分钟),
出租车到达学校站点所需时间为16﹣9﹣1=6(分钟),
出租车的速度为9÷6=1.5(千米/分钟),
两车相遇时出租车出发时间为0.75×(9﹣4)÷(1.5﹣0.75)=5(分钟),
相遇地点离学校站点的路程为9﹣1.5×5=1.5(千米).
答:小刚乘坐出租车出发后经过5分钟追到小强所乘坐的校车,此时他们距学校站点的路程为1.5千米
【解析】(1)根据速度=路程÷时间,可求出校车的速度,再根据m=3+校车速度×(8﹣6),即可求出m的值;(2)根据时间=路程÷速度+4,可求出校车到达学校站点所需时间,进而可求出出租车到达学校站点所需时间,由速度=路程÷时间,可求出出租车的速度,再根据相遇时间=校车先出发时间×速度÷两车速度差,可求出小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车,结合出租车的速度及安康小区到学校站点的路程,可得出相遇时他们距学校站点的路程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】桌面上有四张正面分别标有数字1,2,3,4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗匀.
(1)随机翻开一张卡片,正面所标数字大于2的概率为;
(2)随机翻开一张卡片,从余下的三张卡片中再翻开一张,求翻开的两张卡片正面所标数字之和是偶数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点A处测得正前方小岛C的俯角为30°,面向小岛方向继续飞行10km到达B处,发现小岛在其正后方,此时测得小岛的俯角为45°,如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB与⊙O相切于点B,BC为⊙O的弦,OC⊥OA,OA与BC相交于点P.

(1)求证:AP=AB;
(2)若OB=4,AB=3,求线段BP的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D、F分别在边AB、AC上.

(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形纸片ABCD中,已知AB=1,BC=
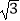 ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.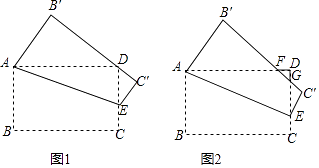
(1)当B′C′恰好经过点D时(如图1),求线段CE的长;
(2)若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°(如图2),求△DFG的面积;
(3)在点E从点C移动到点D的过程中,求点C′运动的路径长. -
科目: 来源: 题型:
查看答案和解析>>【题目】过三点A(2,2),B(6,2),C(4,5)的圆的圆心坐标为( )
A.(4, )
)
B.(4,3)
C.(5, )
)
D.(5,3)
相关试题

