【题目】(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .
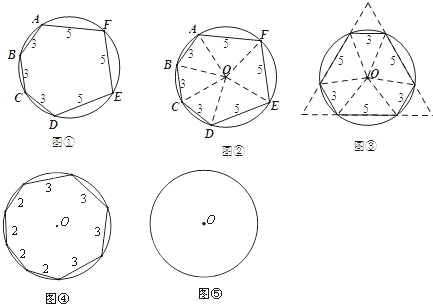
(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.请你仿照小森的思考方式,求出这个八边形的面积.
参考答案:
【答案】(1)![]() (2)13+12
(2)13+12![]() .
.
【解析】
试题分析:(1)如图③,利用六边形ABCDEF每次绕圆心O旋转120°都和原来的图形重合可判断△MNQ为等边三角形,△MAF、△NBC和△QDE都是等边三角形,然后根据等边三角形的面积公式求解;
(2)先画出分割重组的图形,如图⑤,利用八边形ABCDEFGH为轴对称图形,每次绕圆心O旋转90°都和原来的图形重合,可判断四边形PQMN为正方形,△PAB、△GCD、△MEF、△NHG都是等腰直角三角形,根据根据正方形的性质和等腰直角三角形的性质求解.
试题解析:(1)如图③,∵六边形ABCDEF为轴对称图形,每次绕圆心O旋转120°都和原来的图形重合,∴△MNQ为等边三角形,△MAF、△NBC和△QDE都是等边三角形,
∴NQ=3+5+3=11,
∴六边形ABCDEF的面积=S△MNQ﹣3S△AMN
=![]() ×112﹣3×
×112﹣3×![]() ×32
×32
=![]() ;
;
故答案为![]() .
.
(2)如图⑤,∵八边形ABCDEFGH为轴对称图形,每次绕圆心O旋转90°都和原来的图形重合,
∴四边形PQMN为正方形,△PAB、△GCD、△MEF、△NHG都是等腰直角三角形,
∴PA=![]() AB=
AB=![]() ,PN=
,PN=![]() +3+
+3+![]() =3+2
=3+2![]() ,
,
∴这个八边形的面积=(3+2![]() )2﹣4×
)2﹣4×![]() ×
×![]() ×
×![]() =9+12
=9+12![]() +8﹣4=13+12
+8﹣4=13+12![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台)
10
20
30
y(单位:万元∕台)
60
55
50
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本)

-
科目: 来源: 题型:
查看答案和解析>>【题目】点P( 2,-3 )关于x轴的对称点是( )
A. (-2, 3 ) B. (2,3) C. (-2,-3 ) D. (2,-3 )
-
科目: 来源: 题型:
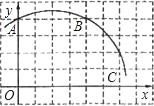
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为 .
(2)连接AD、CD,求⊙D的半径及弧
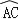 的长.
的长. (3)有一点E(6,0),判断点E与⊙D的位置关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:4x2﹣y2+2y﹣1=___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于任何实数,我们规定符号
 =ad﹣bc,例如:
=ad﹣bc,例如:  =1×4﹣2×3=﹣2
=1×4﹣2×3=﹣2
(1)按照这个规律请你计算 的值;
的值;
(2)按照这个规定请你计算,当a2﹣3a+1=0时,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算a6÷a2的结果是( )
A. a3B. a4C. a8D. a12
相关试题

