【题目】某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:
x(单位:台) | 10 | 20 | 30 |
y(单位:万元∕台) | 60 | 55 | 50 |
(1)求y与x之间的函数关系式,并写出自变量x的取值范围;
(2)求该机器的生产数量;
(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价﹣成本)

参考答案:
【答案】(1)y=﹣![]() x+65(10≤x≤70)(2)50台(3)625万元.
x+65(10≤x≤70)(2)50台(3)625万元.
【解析】
试题分析:(1)设y与x之间的关系式为y=kx+b,运用待定系数法就可以求出其关系式,由该机器生产数量至少为10台,但不超过70台就可以确定自变量的取值范围;
(2)根据每台的成本乘以生产数量等于总成本建立方程求出其解即可;
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z=ma+n,运用待定系数法求出其解析式,再将z=25代入解析式求出a的值,就可以求出每台的利润,从而求出总利润.
试题解析:(1)设y与x之间的关系式为y=kx+b,由题意,得![]() ,
,
解得: ,
,
∴y=﹣![]() x+65.
x+65. ![]()
∵该机器生产数量至少为10台,但不超过70台,
∴10≤x≤70;
(2)由题意,得
xy=2000,
﹣![]() x2+65x=2000,
x2+65x=2000,
﹣x2+130x﹣4000=0,
解得:x1=50,x2=80>70(舍去).
答:该机器的生产数量为50台;
(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z=ma+n,由函数图象,得
![]() ,解得:
,解得:![]() ,∴z=﹣a+90.
,∴z=﹣a+90.
当z=25时,a=65,
成本y=﹣![]() x+65=﹣
x+65=﹣![]() ×50+65=40(万元);
×50+65=40(万元);
总利润为:25(65﹣40)=625(万元).
答:该厂第一个月销售这种机器的利润为625万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据相关部门统计,2014年我国共有9390000名学生参加高考,9390000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明买书需用34元钱,付款时恰好用了1元和5元的纸币共10张,设所用的1元纸币为x张,根据题意,下面所列方程正确的是( )
A. x+10(x-50)=34 B. x+5(10-x)=34 C. x+5(x-10)=34 D. 5x+(10-x)=34
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是数学课堂的一个学习片段, 阅读后, 请回答下面的问题:
学习勾股定理有关内容后, 张老师请同学们交流讨论这样一个问题: “已知直角三角形ABC的两边长分别为3和4, 请你求出第三边.”
同学们经片刻的思考与交流后, 李明同学举手说: “第三边长是5”; 王华同学说: “第三边长是
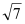 .” 还有一些同学也提出了不同的看法……
.” 还有一些同学也提出了不同的看法……(1)假如你也在课堂上, 你的意见如何? 为什么?
(2)通过上面数学问题的讨论, 你有什么感受? (用一句话表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P( 2,-3 )关于x轴的对称点是( )
A. (-2, 3 ) B. (2,3) C. (-2,-3 ) D. (2,-3 )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:(1)在图中确定该圆弧所在圆的圆心D点的位置,并写出点D点坐标为 .
(2)连接AD、CD,求⊙D的半径及弧
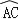 的长.
的长. (3)有一点E(6,0),判断点E与⊙D的位置关系.
-
科目: 来源: 题型:
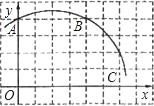
查看答案和解析>>【题目】(1)数学爱好者小森偶然阅读到这样一道竞赛题:
一个圆内接六边形ABCDEF,各边长度依次为 3,3,3,5,5,5,求六边形ABCDEF的面积.
小森利用“同圆中相等的弦所对的圆心角相等”这一数学原理,将六边形进行分割重组,得到图③.可以求出六边形ABCDEF的面积等于 .
(2)类比探究:一个圆内接八边形,各边长度依次为2,2,2,2,3,3,3,3.求这个八边形的面积.请你仿照小森的思考方式,求出这个八边形的面积.
相关试题

