【题目】如图1所示,边长为a的正方形中有一个边长为b的小正方形,图2是由图1中阴影部分拼成的一个长方形,设图1中阴影部分面积为S1,图2中阴影部分面积为S2.
(1)请直接用含a,b的代数式表示S1=______,S2=_____;
(2)写出利用图形的面积关系所揭示的公式:_______;
(3)利用这个公式说明216﹣1既能被15整除,又能被17整除.

参考答案:
【答案】(1)a2﹣b2;(a+b)(a﹣b);(2)a2﹣b2=(a+b)(a﹣b);(3)证明见解析.
【解析】
(1)图1用大正方形的面积去掉小正方形的面积,图2用长方形的面积计算公式;
(2)因为两个图形的阴影部分面积相等,可以根据第(1)问列出等式;
(3)利用所得到的平方差公式分解因式后进行说明.
(1)图1用大正方形的边长为a,小正方形的边长为b,故阴影部分面积为a2﹣b2,图2用长方形的长为(a+b),宽为(a﹣b),故阴影部分面积为(a+b)(a﹣b);
(2)观察图1和图2中阴影部分面积是相等的,故a2﹣b2=(a+b)(a﹣b);
(3)216﹣1=(28﹣1)(28+1)=(24﹣1)(24+1)(28+1)=15×17×(28+1)
因为28+1是整数,故216﹣1既能被15整除,又能被17整除.
-
科目: 来源: 题型:
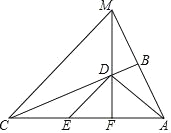
查看答案和解析>>【题目】如图,∠ABC=90°,点D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB的延长线相交于点M,连接MC.
(1)MF与AC的位置关系是:______.
(2)求证:CF=MF.
(3)猜想:AD与MC的位置关系,并说明理由.
-
科目: 来源: 题型:
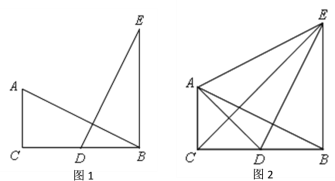
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=90°,AC=
 BC,点D为BC的中点,AB =DE,BE∥AC.
BC,点D为BC的中点,AB =DE,BE∥AC.(1)求证:△ABC≌△DEB;
(2)连结AD、AE、CE,如图2.
①求证:CE是∠ACB的角平分线;
②请判断△ABE是什么特殊形状的三角形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°.
(1)尺规作图:作AB边上的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法和证明);
(2)在(1)的条件下,连接BD,当BC=5cm,AB=13cm时,求△BCD的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
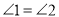 ,
,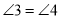 ,
,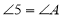 ,试说明:
,试说明: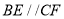 .
.完善下面的解答过程,并填写理由或数学式.
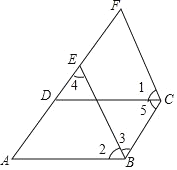
解:因为
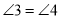 (已知)
(已知)所以
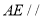 __________.
__________.所以
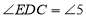 (_________________).
(_________________).因为
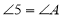 (已知)
(已知)所以
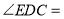 _________.
_________.所以
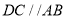 ,
,所以
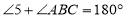 (_______________.)
(_______________.)即:
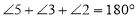 .
.因为
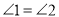 (已知)
(已知)所以
 (___________________.)
(___________________.)即:
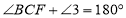 .
.所以
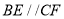 (_____________________.)
(_____________________.) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知正方形ABCD的边长为5,点E在边AB上,AE=3,延长DA至点F,使AF=AE,连结EF.将△AEF绕点A顺时针旋转
 (0°<
(0°< <90°),如图2所示,连结DE、BF.
<90°),如图2所示,连结DE、BF.(1)请直接写出DE的取值范围:_______________________;
(2)试探究DE与BF的数量关系和位置关系,并说明理由;
(3)当DE=4时,求四边形EBCD的面积.

相关试题

