【题目】立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
成绩(m) | 2.35 | 2.4 | 2.45 | 2.5 | 2.55 |
次数 | 1 | 1 | 2 | 5 | 1 |
则下列关于这组数据的说法中正确的是( )
A.众数是2.45
B.平均数是2.45
C.中位数是2.5
D.方差是0.48
参考答案:
【答案】C
【解析】解:A、如图表所示:众数是2.5,故此选项错误; B、平均数是: ![]() (2.35+2.4+2.45×2+2.5×5+2.55)=2.47(m),故此选项错误;
(2.35+2.4+2.45×2+2.5×5+2.55)=2.47(m),故此选项错误;
C、中位数是: ![]() =2.5,故此选项正确;
=2.5,故此选项正确;
D、方差为: ![]() [(2.35﹣2.225)2+(2.4﹣2.225)2+…+(2.55﹣2.225)2]
[(2.35﹣2.225)2+(2.4﹣2.225)2+…+(2.55﹣2.225)2]
= ![]() (0.015625+0.030625+0.050625+0.378125+0.105625)
(0.015625+0.030625+0.050625+0.378125+0.105625)
=0.0580625,故此选项错误;
故选:C.
利用方差的定义、以及众数和中位数的定义分别计算得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正比例函数y=ax的图象与反比例函数y=
 的图象交于点A(3,2)
的图象交于点A(3,2) 
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对称轴为直线x=﹣1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(﹣3,0).
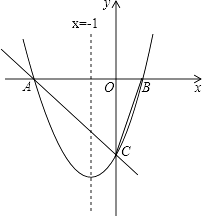
(1)求点B的坐标.
(2)点C是抛物线与y轴的交点,点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.
(1)如图1,当BC=3时,求DM的长.
(2)如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.
①判断四边形AEMD的形状,并说明理由.
②设BC=x(x>0),四边形AEMD的面积为y,试用含x的式子表示y,并说明是否存在x的值,使得四边形AEMD的面积等于△ABC的面积?若存在,请求出x的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的
 ,设人行通道的宽度为x千米,则下列方程正确的是( )
,设人行通道的宽度为x千米,则下列方程正确的是( )
A.(2﹣3x)(1﹣2x)=1
B.
(2﹣3x)(1﹣2x)=1
C.
(2﹣3x)(1﹣2x)=1
D.
(2﹣3x)(1﹣2x)=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )

A.AB=AD
B.AC=BD
C.AD=BC
D.AB=CD -
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )

A.4
B.5
C.5或3
D.4或3
相关试题

