【题目】已知:如图,正比例函数y=ax的图象与反比例函数y= ![]() 的图象交于点A(3,2)
的图象交于点A(3,2) 
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.
参考答案:
【答案】
(1)解:将A(3,2)分别代入y= ![]() ,y=ax得:k=6,a=
,y=ax得:k=6,a= ![]() ,
,
则反比例函数解析式为y= ![]() ,正比例函数解析式为y=
,正比例函数解析式为y= ![]() x;
x;
(2)解:由图象得:在第一象限内,当0<x<3时,反比例函数的值大于一次函数的值;
(3)解:BM=DM,理由为:
∵S△OMB=S△OAC= ![]() ×|k|=3,
×|k|=3,
∴S矩形OBDC=S四边形OADM+S△OMB+S△OAC=3+3+6=12,即OCOB=12,
∵OC=3,∴OB=4,即n=4,
∴m= ![]() =
= ![]() ,
,
∴MB= ![]() ,MD=3﹣
,MD=3﹣ ![]() =
= ![]() ,
,
则MB=MD.
【解析】(1)将A坐标分别代入正比例与反比例函数解析式中求出a与k的值,即可确定出两函数解析式;(2)在图象上找出反比例在正比例上方时x的范围即可;(3)BM=DM,理由为:由反比例函数k的几何意义得到三角形OBM与三角形OAC面积为k的绝对值的一半,求出面积,矩形OBDC的面积=三角形OBM面积+四边形OADM面积+三角形OAC面积,求出矩形OBDC的面积,即为OB与OC的积,由OC的长求出OB的长,即为n的值,将n的值代入反比例解析式中求出m的值,即为BM的长,由BD﹣BM求出MD的长,即可作出判断.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A(2,3)、B(1,1)、C(4,1)是平面直角坐标系中的三点.

(1)①请画出△ABC关于y轴对称的△A1B1C1;
②画出△A1B1C1向下平移3个单位得到的△A2B2C2;
(2)若△ABC中有一点P坐标为(x,y),请直接写出经过以上变换后△A2B2C2中点P的对应点P2的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
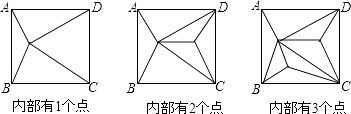
(1)填写如表:正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)如果原正方形被分割成2016个三角形,此时正方形ABCD内部有多少个点?
(3)上述条件下,正方形又能否被分割成2017个三角形?若能,此时正方形ABCD内部有多少个点?若不能,请说明理由.
(4)综上结论,你有什么发现?(写出一条即可) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对称轴为直线x=﹣1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(﹣3,0).
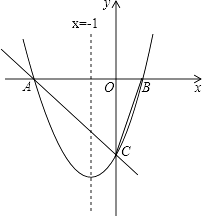
(1)求点B的坐标.
(2)点C是抛物线与y轴的交点,点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.
(1)如图1,当BC=3时,求DM的长.
(2)如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.
①判断四边形AEMD的形状,并说明理由.
②设BC=x(x>0),四边形AEMD的面积为y,试用含x的式子表示y,并说明是否存在x的值,使得四边形AEMD的面积等于△ABC的面积?若存在,请求出x的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
成绩(m)
2.35
2.4
2.45
2.5
2.55
次数
1
1
2
5
1
则下列关于这组数据的说法中正确的是( )
A.众数是2.45
B.平均数是2.45
C.中位数是2.5
D.方差是0.48
相关试题

