【题目】如图,在Rt△ABC中,∠C=90°,AC=6,M、N分别是边AB、AC的中点,在射线MN上取点D,使∠ADM=∠BAC,连接AD.
(1)如图1,当BC=3时,求DM的长.
(2)如图2,以AB为底边在AB的左侧作等腰△ABE,并且使顶角∠AEB=2∠BAC,连接EM.
①判断四边形AEMD的形状,并说明理由.
②设BC=x(x>0),四边形AEMD的面积为y,试用含x的式子表示y,并说明是否存在x的值,使得四边形AEMD的面积等于△ABC的面积?若存在,请求出x的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:如图1中,
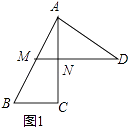
∵AM=MB,AN=NC,
∴MN∥BC,MN= ![]() BC=
BC= ![]() ,
,
∴∠ANM=∠C=90°,
∴∠AMN+∠MAN=90°,
∵∠MAN=∠D,
∴∠AMN+∠D=90°,
∴∠MAD=90°,
∵∠ANM=∠AND=90°,∠MAN=∠D,
∴△MAN∽△ADN,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DN=6,
∴DM=MN+DN= ![]() +6=
+6= ![]() .
.
(2)
解:①如图2中,结论:四边形AEMD是平行四边形.
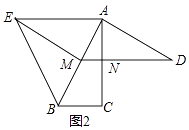
∵EA=EB,AM=BM,
∴EM⊥AB,∠MEB=∠MEA,
由(1)可知AD⊥AB,
∴EM∥AD,
∵∠AEM+∠EAM=90°,
∵∠AEB=2∠BAC,
∴∠AEM=∠BAC,
∴∠BAC+∠EAM=90°,
∴∠EAC=90°=∠MNC,
∴AE∥DM,
∴四边形AEMD是平行四边形.
②∵△MAN∽△ADN,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴DN= ![]() ,
,
∴DM=MN+DN= ![]() +
+ ![]() ,
,
∴S四边形AEMD=DMAN=( ![]() +
+ ![]() )3=
)3= ![]() x+
x+ ![]() .
.
假设存在x,使得四边形AEMD的面积等于△ABC的面积,
则有 ![]() x+
x+ ![]() =
= ![]() x6,
x6,
整理得x2﹣2x+36=0,
∵△=(﹣2)2﹣4×1×36<0,
∴方程无解,假设不成立.
∴不存在使得四边形AEMD的面积等于△ABC的面积的x的值.
【解析】(1)只要证明△MAN∽△ADN,可得 ![]() =
= ![]() ,由此求出DN即可解决问题;(2)①结论:四边形AEMD是平行四边形.分别证明EM∥AD,AE∥DM即可;②由△MAN∽△ADN,可得
,由此求出DN即可解决问题;(2)①结论:四边形AEMD是平行四边形.分别证明EM∥AD,AE∥DM即可;②由△MAN∽△ADN,可得 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,求出DN,即可解决问题.利用反证法证明不存在x的值,使得四边形AEMD的面积等于△ABC的面积;
,求出DN,即可解决问题.利用反证法证明不存在x的值,使得四边形AEMD的面积等于△ABC的面积;
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,从点A看一山坡上的电线杆PQ,观测点P的仰角是45°,向前走6m到达B点,测得顶端点P和杆底端点Q的仰角分别是60°和30°,求该电线杆PQ的高度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,正比例函数y=ax的图象与反比例函数y=
 的图象交于点A(3,2)
的图象交于点A(3,2) 
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】对称轴为直线x=﹣1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(﹣3,0).
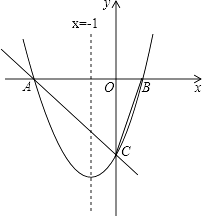
(1)求点B的坐标.
(2)点C是抛物线与y轴的交点,点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】立定跳远是小刚同学体育中考的选考项目之一.某次体育课上,体育老师记录了小刚的一组立定跳远训练成绩如下表:
成绩(m)
2.35
2.4
2.45
2.5
2.55
次数
1
1
2
5
1
则下列关于这组数据的说法中正确的是( )
A.众数是2.45
B.平均数是2.45
C.中位数是2.5
D.方差是0.48 -
科目: 来源: 题型:
查看答案和解析>>【题目】某广场绿化工程中有一块长2千米,宽1千米的矩形空地,计划在其中修建两块相同的矩形绿地,两块绿地之间既周边留有宽度相等的人行通道(如图),并在这些人行通道铺上瓷砖,要求铺瓷砖的面积是矩形空地面积的
 ,设人行通道的宽度为x千米,则下列方程正确的是( )
,设人行通道的宽度为x千米,则下列方程正确的是( )
A.(2﹣3x)(1﹣2x)=1
B.
(2﹣3x)(1﹣2x)=1
C.
(2﹣3x)(1﹣2x)=1
D.
(2﹣3x)(1﹣2x)=2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是( )

A.AB=AD
B.AC=BD
C.AD=BC
D.AB=CD
相关试题

